题目内容
如图,正方形OABC的边长为2.(1)在其四边或内部取点P(x,y),且x,y∈Z,求事件“|OP|>1”的概率;
(2)在其内部取点P(x,y),且x,y∈R,求事件“△POA,△PAB,△PBC,△PCO的面积均大于
 ”的概率是.
”的概率是.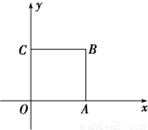
【答案】分析:(1)分析出正方形的四边和内部取点P(x,y),且x,y∈Z的全部基本事件个数,及满足“|OP|>1”的基本事件个数,代入古典概型公式可得事件“|OP|>1”的概率;
(2)求出满足条件的所有基本事件对应的平面区域Ω的面积,及满足条件“△POA,△PAB,△PBC,△PCO的面积均大于 的平面区域面积,代入几何概型公式,可得事件“△POA,△PAB,△PBC,△PCO的面积均大于
的平面区域面积,代入几何概型公式,可得事件“△POA,△PAB,△PBC,△PCO的面积均大于 ”的概率
”的概率
解答:解:(1)在正方形的四边和内部取点P(x,y),且x,y∈Z,所有可能的事件是
(0,0),(0,1),(0,2),(1,0),(1,1),
(1,2),(2,0),(2,1),(2,2),
其中满足|OP|>1的事件是
(0,2),(1,1),(1,2),(2,0),(2,1),(2,2),
所以满足|OP|>1的概率为 .(6分)
.(6分)
(2)在正方形内部取点,其总的事件包含的区域面积为4,
由于各边长为2,
所以要使△POA,△PAB,△PBC,△PCO的面积均大于 ,
,
应该三角形的高大于 ,
,
所以这个区域为每个边长从两端各去掉 后剩余的正方形,
后剩余的正方形,
其面积为 ×
× =
= ,
,
所以满足条件的概率为 .(12分)
.(12分)
点评:本题考查的知识点是几何概型,及古典概型,其中求出所有基本事件个数(对应区域面积)和满足条件的基本事件个数(对应区域面积)是解答的关键.
(2)求出满足条件的所有基本事件对应的平面区域Ω的面积,及满足条件“△POA,△PAB,△PBC,△PCO的面积均大于
 的平面区域面积,代入几何概型公式,可得事件“△POA,△PAB,△PBC,△PCO的面积均大于
的平面区域面积,代入几何概型公式,可得事件“△POA,△PAB,△PBC,△PCO的面积均大于 ”的概率
”的概率解答:解:(1)在正方形的四边和内部取点P(x,y),且x,y∈Z,所有可能的事件是
(0,0),(0,1),(0,2),(1,0),(1,1),
(1,2),(2,0),(2,1),(2,2),
其中满足|OP|>1的事件是
(0,2),(1,1),(1,2),(2,0),(2,1),(2,2),
所以满足|OP|>1的概率为
 .(6分)
.(6分)(2)在正方形内部取点,其总的事件包含的区域面积为4,
由于各边长为2,
所以要使△POA,△PAB,△PBC,△PCO的面积均大于
 ,
,应该三角形的高大于
 ,
,所以这个区域为每个边长从两端各去掉
 后剩余的正方形,
后剩余的正方形,其面积为
 ×
× =
= ,
,所以满足条件的概率为
 .(12分)
.(12分)点评:本题考查的知识点是几何概型,及古典概型,其中求出所有基本事件个数(对应区域面积)和满足条件的基本事件个数(对应区域面积)是解答的关键.

练习册系列答案
相关题目
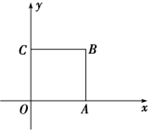 如图,正方形OABC的边长为2.
如图,正方形OABC的边长为2.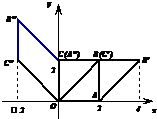 (Ⅰ)如图,正方形OABC在二阶矩阵M对应的切变变换作用下变为平行四边形OA′B′C′,平行四边形OA'B'C'在二阶矩阵N对应的旋转变换作用下变为平行四边形OA''B''C'',求将正方形OABC变为平行四边形OA''B''C''的变换对应的矩阵.
(Ⅰ)如图,正方形OABC在二阶矩阵M对应的切变变换作用下变为平行四边形OA′B′C′,平行四边形OA'B'C'在二阶矩阵N对应的旋转变换作用下变为平行四边形OA''B''C'',求将正方形OABC变为平行四边形OA''B''C''的变换对应的矩阵. 如图,正方形OABC是某个四边形的直观图,若OA=1,则原四边形的面积为
如图,正方形OABC是某个四边形的直观图,若OA=1,则原四边形的面积为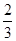 ”的概率是________.
”的概率是________.