题目内容
在三角形ABC中,∠A,∠B,∠C所对的边长分别为a,b,c,其外接圆的半径 ,则
,则 的最小值为 ________.
的最小值为 ________.

分析:先利用正弦定理用a,b和c以及R分别表示出sinA,sinB,sinC,进而把原式展开后利用基本不等式求得其最小值.
解答:由正弦定理可知
 =2R
=2R∴sinA=
 ,sinB=
,sinB= ,sinC=
,sinC=
∴

=4R2(a2+b2+c2)(
 )
)=4R2(3+
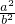 +
+ +
+ +
+ +
+ +
+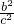 )≥4R2(3+2+2+2)=
)≥4R2(3+2+2+2)= (当且仅当a=b=c时等号成立).
(当且仅当a=b=c时等号成立).故答案为:

点评:本题主要考查了正弦定理的应用,基本不等式在最值问题中的应用.解题的关键是利用正弦定理把问题转化为边的问题,进行解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在三角形ABC中,A=120°,AB=5,BC=7,则
的值为( )
| sinB |
| sinC |
A、
| ||
B、
| ||
C、
| ||
D、
|