题目内容

若m，n，m+n成等差数列，m，n，m•n成等比数列，则椭圆
x2
m
+
y2
n
=1的离心率为（　　）
分析：利用m，n，m+n成等差数列，m，n，m•n成等比数列，推出m，n的关系，然后求解椭圆
x2
m
+
y2
n
=1的离心率即可．
解答：解：由题意m，n，m+n成等差数列，知2n=m+m+n∴n=2m，
m，n，m•n成等比数列，n2=m•m•n，∴n=m2，∴m2=2m
∴m=2，∴n=4，又椭圆
x2
m
+
y2
n
=1
∴a2=4，b2=2，c2=2
∴e=
c
a
=
2
2

故选B
点评：本题考查等差数列，成等比数列的中项公式的应用，椭圆
x2
m
+
y2
n
=1的离心率的求法，考查计算能力．
练习册系列答案
相关题目
设m个不全相等的正数a1，a2，…，am（m≥7）依次围成一个圆圈，
（Ⅰ）若m=2009，且a1，a2，…，a1005是公差为d的等差数列，而a1，a2009，a2008，…，a1006是公比为q=d的等比数列；数列a1，a2，…，am的前n项和Sn（n≤m）满足：S3=15，S2009=S2007+12a1，求通项an（n≤m）；
（Ⅱ）若每个数an（n≤m）是其左右相邻两数平方的等比中项，求证：a1+…+a6+a72+…+am2＞ma1a2am．
下列命题中正确的有（　　）
①若向量a与b满足a•b＜0，则a与b所成角为钝角；
②若向量a与b不共线，m=λ1•a+λ2•b，n=μ1•a+μ2•b，（λ1，λ2μ1，μ2∈R），则m∥n的充要条件是λ1•μ2-λ2•μ1=0；
③若
OA 
+
OB
+
OC 
=0，且|
OA 
|=|
OB
|=|
OC 
|，则△ABC是等边三角形；
④若a与b非零向量，a⊥b，则|a+b|=|a-b|．
A、②③④B、①②③C、①④D、②
下列命题中正确的有
②③④
②③④
（填序号）
①若
a
与
b
满足
a
•
b
＞0，则
a
与
b
所成的角为锐角；
②若
a
与
b
不共线，
m
=λ1
a
+λ2
b
，
n
=μ1
a
+μ2
b
（λ1，λ2，μ1，μ2∈R），则
m
∥
n
的充要条件是λ1μ2-λ2μ1=0；
③若
OA
+
OB
+
OC
=
O
，且|
OA
|=|
OB
|=|
OC
|，则△ABC是等边三角形；
④若
a
与
b
为非零向量，且
a
⊥
b
，则|
a
+
b
|=|
a
-
b
|；
⑤设
a
，
b
，
c
为非零向量，若
a
•
b
=
c
•
b
，则
a
=
c
；
⑥若
a
，
b
，
c
为非零向量，则
a
•(
b
•
c
)=(
a
•
b
)•
c
．
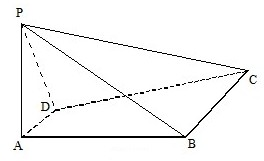精英家教网如图，四棱锥P-ABCD中，PA⊥平面ABCD，四边形ABCD是直角梯形，其中DA⊥AB，AD∥BC．PA=2AD=BC=2AB=2
2
．
（1）求异面直线PC与AD所成角的大小；
（2）若平面ABCD内有一经过点C的曲线E，该曲线上的任一动点Q都满足PQ与AD所成角的大小恰等PC与AD所成角．试判断曲线E的形状并说明理由；
（3）在平面ABCD内，设点Q是（2）题中的曲线E在直角梯形ABCD内部（包括边界）的一段曲线CG上的动点，其中G为曲线E和DC的交点．以B为圆心，BQ为半径的圆分别与梯形的边AB、BC交于M、N两点．当Q点在曲线段GC上运动时，试提出一个研究有关四面P-BMN的问题（如体积、线面、面面关系等）并尝试解决．
（说明：本小题将根据你提出的问题的质量和解决难度分层评分；本小题的计算结果可以使用近似值，保留3位小数）

设m个不全相等的正数a1，a2，…，am(m≥7)依次围成一个圆圈．

(Ⅰ)若m＝2009，且a1，a2，…，a1005是公差为d的等差数列，而a1，a2009，a2008，…，a1006是公比为q＝d的等比数列；数列a1，a2，…，am的前n项和Sn(n≤m)满足：S3＝15，S2009＝S2007＋12a1，求通项an(n≤m)；

(Ⅱ)若每个数an(n≤m)是其左右相邻两数平方的等比中项，求证：；

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网