题目内容
已知两点![]() ,点
,点![]() 为坐标平面内的动点,满足
为坐标平面内的动点,满足![]() =0,则动点
=0,则动点![]() 到两点
到两点![]() 、
、![]() 的距离之和的最小值为 ( )
的距离之和的最小值为 ( )
A.4 B.5 C.6 D.![]()
解析:B。设![]() ,因为
,因为![]() ,所以
,所以![]()
则![]()
由![]() ,则
,则![]() ,
,
化简整理得![]() ,所以点A是抛物线
,所以点A是抛物线![]() 的焦点,点B在抛物线的内部,所以点P到A、B两点的最短距离之和就是点B到准线
的焦点,点B在抛物线的内部,所以点P到A、B两点的最短距离之和就是点B到准线![]() 的距离,
的距离,
所以![]()
解题探究:本题在向量与圆锥曲线交汇处命题,考查了向量的数量积、曲线方程的求法、抛物线的定义以及等价转化能力。首先利用向量数量积的运算求出抛物线的方程,然后再利用抛物线的定义将动点![]() 到两点
到两点![]() 、
、![]() 的距离之和转化为点B到准线
的距离之和转化为点B到准线![]() 的距离。
的距离。

练习册系列答案
相关题目
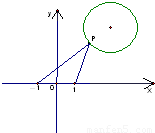
 如图平面上有A(1,0),B(-1,0)两点,已知圆的方程为(x-3)2+(y-4)2=22.
如图平面上有A(1,0),B(-1,0)两点,已知圆的方程为(x-3)2+(y-4)2=22.