题目内容
已知函数f(x)=2sinx•cosx+2cos2x
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)请用“五点法”作出函数f(x)在区间[-
,
]上的简图.
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)请用“五点法”作出函数f(x)在区间[-
| π |
| 8 |
| 7π |
| 8 |
分析:(Ⅰ)函数解析式第一项利用二倍角的正弦 函数公式化简,第二项利用二倍角的余弦函数公式化简,整理后再利用两角和与差的正弦函数公式化为一个角的正弦函数,找出ω的值,代入周期公式即可确定出函数f(x)的最小正周期;
(Ⅱ)根据x的范围求出这个角的范围,利用“五点法”作出f(x)的草图即可.
(Ⅱ)根据x的范围求出这个角的范围,利用“五点法”作出f(x)的草图即可.
解答:解:(Ⅰ)f(x)=sin2x+cos2x+1=
(
sin2x+
cos2x)=
sin(2x+
)+1,
∵ω=2,∴T=π,
则函数f(x)的最小正周期为π;
(Ⅱ)∵x∈[-
,
],∴2x+
∈[0,2π],
列表如下:
作出图象,如图所示:
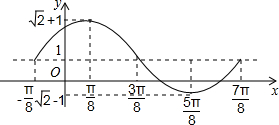 .
.
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| π |
| 4 |
∵ω=2,∴T=π,
则函数f(x)的最小正周期为π;
(Ⅱ)∵x∈[-
| π |
| 8 |
| 7π |
| 8 |
| π |
| 4 |
列表如下:
| x | -
|
|
|
|
| ||||||||||
2x+
|
0 |
|
π |
|
2π | ||||||||||
| y=f(x) | 1 |
|
1 |
|
1 |
 .
.点评:此题考查了两角和与差的正弦函数公式,二倍角的正弦、余弦函数公式,三角函数的周期性及其求法,熟练掌握公式是解本题的关键.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目