题目内容
已知二次函数f(x)=ax2+bx,f(x﹣1)为偶函数,集合A={x|f(x)=x}为单元素集合.
(Ⅰ)求f(x)的解析式;
(Ⅱ)设函数g(x)=[f(x)﹣m] ex,若函数g(x)在x∈[﹣3,2]上单调,求实数m的取值范围.
ex,若函数g(x)在x∈[﹣3,2]上单调,求实数m的取值范围.
(Ⅰ)求f(x)的解析式;
(Ⅱ)设函数g(x)=[f(x)﹣m]
 ex,若函数g(x)在x∈[﹣3,2]上单调,求实数m的取值范围.
ex,若函数g(x)在x∈[﹣3,2]上单调,求实数m的取值范围. 解:(Ⅰ)∵二次函数f(x)=ax2+bx,f(x﹣1)为偶函数,
∴f(x)的对称轴为x=﹣1,
∴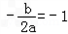
∵集合A={x|f(x)=x}为单元素集合
∴f(x)=x有两个相等的实数根
∴ax2+(b﹣1)x=0,
∴b=1
∴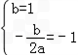
∴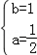
∴f(x)的解析式为f(x)= x2+x;
x2+x;
(Ⅱ)g(x)=( x2+x﹣m)ex,若函数g(x)在x∈[﹣3,2]上单调递增,
x2+x﹣m)ex,若函数g(x)在x∈[﹣3,2]上单调递增,
则g'(x)≥0在x∈[﹣3,2]上恒成立
即( x2+x+1﹣m)ex≥0对x∈[﹣3,2]上恒成立
x2+x+1﹣m)ex≥0对x∈[﹣3,2]上恒成立
∴m≤( x2+x+1)min(x∈[﹣3,2])
x2+x+1)min(x∈[﹣3,2])
∴m≤﹣1 若函数g(x)在x∈[﹣3,2]上单调递减,则g′(x)≤0在x∈[﹣3,2]上恒成立
即( x2+x+1﹣m) ex≤0对x∈[﹣3,2]上恒成立
ex≤0对x∈[﹣3,2]上恒成立
∴m≥( x2+x+1)max(x∈[﹣3,2])
∴m≥7
∴实数m的取值范围为(﹣∞,﹣1]∪[7,+∞).
∴f(x)的对称轴为x=﹣1,
∴
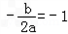
∵集合A={x|f(x)=x}为单元素集合
∴f(x)=x有两个相等的实数根
∴ax2+(b﹣1)x=0,
∴b=1
∴
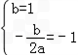
∴
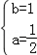
∴f(x)的解析式为f(x)=
 x2+x;
x2+x;(Ⅱ)g(x)=(
 x2+x﹣m)ex,若函数g(x)在x∈[﹣3,2]上单调递增,
x2+x﹣m)ex,若函数g(x)在x∈[﹣3,2]上单调递增,则g'(x)≥0在x∈[﹣3,2]上恒成立
即(
 x2+x+1﹣m)ex≥0对x∈[﹣3,2]上恒成立
x2+x+1﹣m)ex≥0对x∈[﹣3,2]上恒成立∴m≤(
 x2+x+1)min(x∈[﹣3,2])
x2+x+1)min(x∈[﹣3,2])∴m≤﹣1 若函数g(x)在x∈[﹣3,2]上单调递减,则g′(x)≤0在x∈[﹣3,2]上恒成立
即( x2+x+1﹣m)
 ex≤0对x∈[﹣3,2]上恒成立
ex≤0对x∈[﹣3,2]上恒成立 ∴m≥( x2+x+1)max(x∈[﹣3,2])
∴m≥7
∴实数m的取值范围为(﹣∞,﹣1]∪[7,+∞).

练习册系列答案
相关题目