题目内容
已知数列{an}满足条件: .
.
(Ⅰ)求证:数列{an+1}为等比数列;
(Ⅱ)若bn=(2n-1)(an+1),求数列{bn}的前n项和Tn.
(Ⅰ)证明:由题意得an+1+1=2(an+1),…(3分)
又a1+1=2≠0. …(4分)
所以数列{an+1}是以2为首项,2为公比的等比数列. …(5分)
(Ⅱ)解:由(1)知 即
即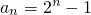 ,…(7分)
,…(7分)
故
∴Tn=b1+b2+b3+…+bn
=1•2+3•22+5•23+…+(2n-1)2n
2Tn=1•22+3•23+5•24+…+(2n-1)2n+1…(8分)
错位相减得-Tn=2+2•22+2•23+2•24+…+2•2n-(2n-1)2n+1…(9分)
= =(3-2n)2n+1-6…(11分)
=(3-2n)2n+1-6…(11分)
从而得Tn=(2n-3)2n+1+6…(12分)
分析:(Ⅰ)由题意得an+1+1=2(an+1)可证数列{an+1}是以等比数列.
(Ⅱ)由(1)可求即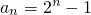 ,
, ,结合数列的特点,故考虑利用错位相减求和
,结合数列的特点,故考虑利用错位相减求和
点评:本题主要考查了利用数列的递推公式an+1=pan+q构造等比数列求解数列的通项,错位相减求和的方法要求掌握,并且还要知道其方法适用的数列类型
又a1+1=2≠0. …(4分)
所以数列{an+1}是以2为首项,2为公比的等比数列. …(5分)
(Ⅱ)解:由(1)知
 即
即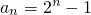 ,…(7分)
,…(7分)故

∴Tn=b1+b2+b3+…+bn
=1•2+3•22+5•23+…+(2n-1)2n
2Tn=1•22+3•23+5•24+…+(2n-1)2n+1…(8分)
错位相减得-Tn=2+2•22+2•23+2•24+…+2•2n-(2n-1)2n+1…(9分)
=
 =(3-2n)2n+1-6…(11分)
=(3-2n)2n+1-6…(11分)从而得Tn=(2n-3)2n+1+6…(12分)
分析:(Ⅰ)由题意得an+1+1=2(an+1)可证数列{an+1}是以等比数列.
(Ⅱ)由(1)可求即
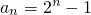 ,
, ,结合数列的特点,故考虑利用错位相减求和
,结合数列的特点,故考虑利用错位相减求和点评:本题主要考查了利用数列的递推公式an+1=pan+q构造等比数列求解数列的通项,错位相减求和的方法要求掌握,并且还要知道其方法适用的数列类型

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目