题目内容
(理)对于任意实数a、b,不等式max{|a+b|,|a-b|,|2006-b|}≥C恒成立,则常数C的最大值是 ______.(注:max,y,z表示x,y,z中的最大者.)
(文)不等式
≥0的解集是 ______.
(文)不等式
| 5-x |
| 5x+2 |
(理)设M=max{|a+b|,|a-b|,|2006-b|}
则M≥|a+b|;M≥|b-a|;2M≥|4012-2b|
相加得
4M≥|a+b|+|b-a|+|4012-2b|≥|a+b+b-a+4012-2b|=4012
即M≥1003
当a+b,b-a,4012-2b同号时取等号
即当a=0,b=1003时M=1003,等号成立,即M的最小值为1003,
也即C的最大值为1003
(文)
≥0即
≤0
∴-
<x≤5
故不等式的解集为{x|-
<x≤5}
故答案为1003;{x|-
<x≤5}
则M≥|a+b|;M≥|b-a|;2M≥|4012-2b|
相加得
4M≥|a+b|+|b-a|+|4012-2b|≥|a+b+b-a+4012-2b|=4012
即M≥1003
当a+b,b-a,4012-2b同号时取等号
即当a=0,b=1003时M=1003,等号成立,即M的最小值为1003,
也即C的最大值为1003
(文)
| 5-x |
| 5x+2 |
| x-5 |
| 5x+2 |
∴-
| 2 |
| 5 |
故不等式的解集为{x|-
| 2 |
| 5 |
故答案为1003;{x|-
| 2 |
| 5 |

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
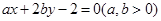 始终平分圆
始终平分圆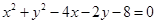 的周长,则
的周长,则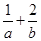 的最小值为 ( )
的最小值为 ( )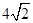
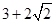
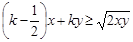 恒成立,则实数
恒成立,则实数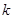 的最小值是 ( )
的最小值是 ( )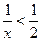 的解集是( )
的解集是( )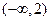
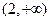
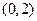
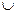

 ,则不等式右端
,则不等式右端 的表达式应为 *** .
的表达式应为 *** .