题目内容
已知锐角α、β满足tanα=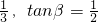 ,则α+β的值为
,则α+β的值为
- A.30°
- B.45°
- C.60°
- D.90°
B
分析:由已知中角α、β满足tanα=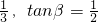 ,我们代入两角和的正切公式,可以求出α+β的正切值,根据α、β为锐角,我们易得α+β的值.
,我们代入两角和的正切公式,可以求出α+β的正切值,根据α、β为锐角,我们易得α+β的值.
解答:∵锐角α、β满足tanα=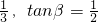 ,
,
∴tan(α+β)= =
= =1
=1
故α+β=45°
故选B
点评:本题考查的知识点是两角和的正切函数,其中根据α、β为锐角,确定α+β的范围是解答本题的关键.
分析:由已知中角α、β满足tanα=
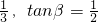 ,我们代入两角和的正切公式,可以求出α+β的正切值,根据α、β为锐角,我们易得α+β的值.
,我们代入两角和的正切公式,可以求出α+β的正切值,根据α、β为锐角,我们易得α+β的值.解答:∵锐角α、β满足tanα=
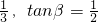 ,
,∴tan(α+β)=
 =
= =1
=1故α+β=45°
故选B
点评:本题考查的知识点是两角和的正切函数,其中根据α、β为锐角,确定α+β的范围是解答本题的关键.

练习册系列答案
 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 ,且
,且 =1,
=1,
 .
. (文)如图,|AB|=2,O为AB中点,直线
(文)如图,|AB|=2,O为AB中点,直线 过B且垂直于AB,过A的动直线与
过B且垂直于AB,过A的动直线与