题目内容
已知数列2010，2011，1，-2010，-2011，…，这个数列的特点是从第二项起，每一项都等于它的前后两项之和，则这个数列的前2011项之和S2011等于
2011
2011
．分析：由数列的规律可得该数列是以6为周期，且，a1+a2+a3+a4+a5+a6=0，从而可求数列的和
解答：解：由题意可得，a1+a2+a3+a4+a5+a6=0，
且a1=a7=a13=…a2010，a2011=a2=2011
∴S2011=a1+a2+a3+…+a2011
=（a1+…+a6）+…+（a2005+…+a2010）+a2011
=2011
故答案为：2011
且a1=a7=a13=…a2010，a2011=a2=2011
∴S2011=a1+a2+a3+…+a2011
=（a1+…+a6）+…+（a2005+…+a2010）+a2011
=2011
故答案为：2011
点评：本题主要考查了数列的和的求解，解决本题的关键有2个，一是要能发现该数列以6 为周期，二是要能发现，a1+a2+a3+a4+a5+a6=0
练习册系列答案
相关题目
的前n项和为
，令
，称
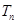为数列
，
，…，
的“理想数”，已知数列
的“理想数”为2012，那么数列2，
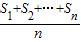，则称Tn为数列a1，a2，…，an的“理想数”，已知数列a1，a2，…，a2009的“理想数”为2010，那么数列2，a1，a2，…，a2009 的“理想数”为 ．
，则称Tn为数列a1，a2，…，an的“理想数”，已知数列a1，a2，…，a2009的“理想数”为2010，那么数列2，a1，a2，…，a2009 的“理想数”为 ．
，称Tn为数列a1，a2，…，an的“理想数”，已知数列a1，a2，…，a2009的“理想数”为2010，那么数列2，a1，a2，…，a2009的“理想数”为（ ）。