题目内容
如图,在四棱锥 中,底面
中,底面 是矩形,
是矩形,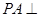 平面
平面 ,
, ,
, ,
, 依次是
依次是 的中点.
的中点.
(1)求证: ;
;
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(1)∵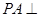 平面
平面 ,底面
,底面 是矩形,
是矩形,
∴ 平面
平面 ,∴
,∴ .∵
.∵ 是
是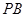 的中点,
的中点,  ∴
∴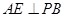 ,∵
,∵ ,∴
,∴ ;(2)直线
;(2)直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 .
.
解析试题分析:(1)要证明直线 ,即证明直线
,即证明直线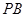 与平面
与平面 的两条相交的直线垂直,即证明
的两条相交的直线垂直,即证明 和
和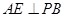 即可;(2)由题意知
即可;(2)由题意知 平面
平面 ,取
,取 中点
中点 ,
, 中点
中点 ,联结
,联结 ,则确定直线
,则确定直线 与平面
与平面 所成的角即为
所成的角即为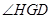 ,在
,在 中,易求出直线
中,易求出直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
试题解析:(1)∵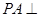 平面
平面 ,底面
,底面 是矩形
是矩形
∴ 平面
平面 ∴
∴
∵ 是
是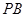 的中点
的中点  ∴
∴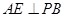
∵ ∴
∴

(2)∵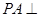 平面
平面 ,∴
,∴ ,
,
又 ,∴
,∴ 平面
平面 ,
,
取 中点
中点 ,
, 中点
中点 ,联结
,联结 ,
,
则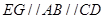 且
且 ,
,
∴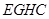 是平行四边形,∴
是平行四边形,∴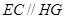
∴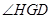 即为直线
即为直线 与平面
与平面 所成的角.
所成的角.
在 中,
中, ,
,  ,
,
∴直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 .
.
考点:线面垂直;直线与平面所成的角.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 为斜三棱柱
为斜三棱柱 的侧棱
的侧棱 上一点,
上一点,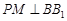 交
交 于点
于点 ,
, 交
交 于点
于点 .
.
 ;
; 中有余弦定理:
中有余弦定理: .
. -A BC中,AB
-A BC中,AB 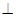 AC, AB=AC=2,
AC, AB=AC=2,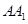 =4,点D是BC的中点.
=4,点D是BC的中点.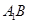 与
与 所成角的余弦值;
所成角的余弦值; 与
与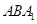 所成二面角的正弦值.
所成二面角的正弦值.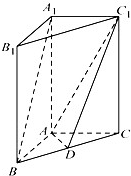
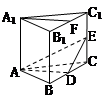
 ,BC=,求二面角S-AB-C的余弦值.
,BC=,求二面角S-AB-C的余弦值.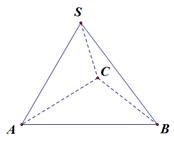
 中,点
中,点 分别是棱
分别是棱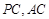 的中点.
的中点.  //平面
//平面 ;
; 平面
平面 ,
, ,求证:
,求证: .
.

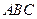 —
—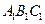 中,侧棱垂直底面,
中,侧棱垂直底面, ,
,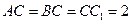 。
。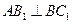 ;
; —
—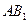 —
—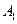 的大小。
的大小。 ,那么b与c夹角是
,那么b与c夹角是 