题目内容
(本小题满分12分)已知函数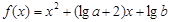 满足
满足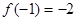 , 且对于任意
, 且对于任意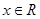 ,恒有
,恒有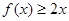 成立.(1)求实数
成立.(1)求实数 的值;
的值;
(2)解不等式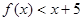 .
.
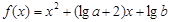 满足
满足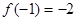 , 且对于任意
, 且对于任意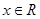 ,恒有
,恒有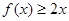 成立.(1)求实数
成立.(1)求实数 的值;
的值; (2)解不等式
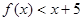 .
.(1)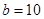 ,
, 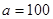 . (2)
. (2) 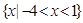 .
.
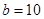 ,
, 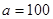 . (2)
. (2) 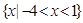 .
.(1)由f(-1)=-2,代入函数解析式得到关于lga与lgb的等式记作①,化简后得到关于a与b的等式记作②,又因为f(x)≥2x恒成立,把f(x)的解析式代入后,令△≤0得到关于lga与lgb的不等式,把①代入后得到关于lgb的不等式,根据平方大于等于0,即可求出b的值,把b的值代入②即可求出a的值;
(2)由(1)求出的a与b的值代入f(x)的解析式中即可确定出f(x)的解析式,然后把f(x)的解析式代入到f(x)<x+5中,得到关于x的一元二次不等式,求出一元二次不等式的解集即可.
解:(1)由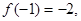 知
知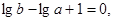 ∴
∴ 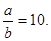
又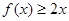 恒成立, 所以
恒成立, 所以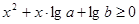 恒成立,
恒成立,
故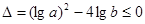 . 将
. 将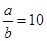 代入得:
代入得: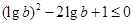 , 即
, 即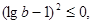 即
即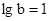 .故
.故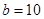 , 所以
, 所以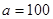 .
.
(2) 因为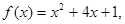 所以
所以 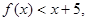 即
即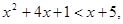
∴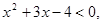 所以
所以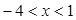 , ∴不等式的解集为
, ∴不等式的解集为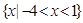 .
.
(2)由(1)求出的a与b的值代入f(x)的解析式中即可确定出f(x)的解析式,然后把f(x)的解析式代入到f(x)<x+5中,得到关于x的一元二次不等式,求出一元二次不等式的解集即可.
解:(1)由
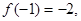 知
知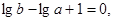 ∴
∴ 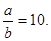
又
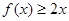 恒成立, 所以
恒成立, 所以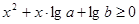 恒成立,
恒成立,故
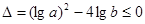 . 将
. 将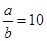 代入得:
代入得: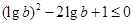 , 即
, 即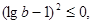 即
即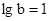 .故
.故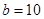 , 所以
, 所以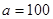 .
. (2) 因为
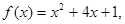 所以
所以 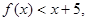 即
即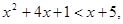
∴
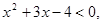 所以
所以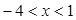 , ∴不等式的解集为
, ∴不等式的解集为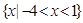 .
.
练习册系列答案
相关题目
 的不等式
的不等式 .
.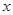 的不等式
的不等式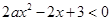 的解集为(2,
的解集为(2,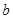 ),则
),则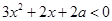 的解集为 .
的解集为 .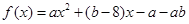 ,当
,当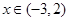 时,
时,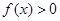 ;
;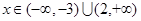 时,
时,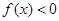 .
.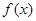 在
在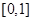 内的值域;
内的值域;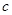 为何值时,
为何值时,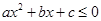 的解集为
的解集为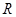 .
. 的不等式:
的不等式:
 ⊙
⊙
 ,则满足
,则满足 ⊙
⊙ 的实数
的实数 的解集是( )
的解集是( )


