题目内容
△ABC中，AD为角平分线，E为AD的中点，BE交AC于F，若| AB |
| a |
| AC |
| b |
| a |
| b |
| a |
| b |
| AD |
| BE |
| BF |
分析：先利用角平分线定理得
=
，进而利用向量加法的三角形法则，将
用基底表示，由于E为AD的中点，由向量加法的平行四边形法则可将
用基底表示，最后用待定系数法，设
=λ
=-
λ
+
λ
，再利用A、F、C三点共线，又得
=-
+μ
，利用向量相等的概念和平面向量基本定理列方程即可解得λ，μ值，从而将
用基底表示
| BD |
| 2 |
| 3 |
| BC |
| AD |
| BE |
| BF |
| BE |
| 5 |
| 6 |
| a |
| 1 |
| 3 |
| b |
| BF |
| a |
| b |
| BF |
解答：解：由角平分线定理得
=
=2，∴
=
=
（
-
）
∴
=
+
=
+
(
-
)=
+
∴
=
(
+
)=
+
(
-
)=-
+
(
+
-
)=-
+
设
=λ
=-
λ
+
λ
，又
=
+
=-
+μ
=-
+μ
∴
，解得
，
∴
=-
+
| AB |
| AC |
| BD |
| DC |
| BD |
| 2 |
| 3 |
| BC |
| 2 |
| 3 |
| b |
| a |
∴
| AD |
| AB |
| BD |
| a |
| 2 |
| 3 |
| AC |
| AB |
| 1 |
| 3 |
| a |
| 2 |
| 3 |
| b |
∴
| BE |
| 1 |
| 2 |
| BA |
| BD |
| 1 |
| 2 |
| BA |
| 1 |
| 2 |
| AD |
| AB |
| 1 |
| 2 |
| a |
| 1 |
| 2 |
| 1 |
| 3 |
| a |
| 2 |
| 3 |
| b |
| a |
| 5 |
| 6 |
| a |
| 1 |
| 3 |
| b |
设
| BF |
| BE |
| 5 |
| 6 |
| a |
| 1 |
| 3 |
| b |
| BF |
| BA |
| AF |
| a |
| AC |
| a |
| b |
∴
|
|
∴
| BF |
| a |
| 2 |
| 5 |
| b |
点评：本题考查了平面向量基本定理的应用，利用向量加法的三角形法则和平行四边形法则将平面向量用一组基底表示的方法和技巧
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
，若
，
且
，
，用
、
表示
，
，
△ABC中，AD为角平分线，E为AD的中点，BE交AC于F，若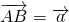
，
且
，
，用
、
表示
，
，
．
，
且
，
，用
、
表示
，
，
．
，
且
，
，用
、
表示
，
，
．