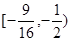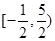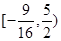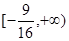题目内容
定义在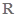 上的单调函数
上的单调函数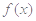 满足
满足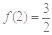 ,且对任意
,且对任意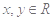 都有
都有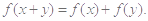
(1)求证: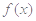 为奇函数;
为奇函数;
(2)若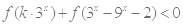 对任意
对任意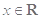 恒成立,求实数
恒成立,求实数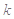 的取值范围.
的取值范围.
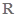 上的单调函数
上的单调函数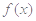 满足
满足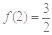 ,且对任意
,且对任意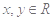 都有
都有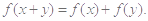
(1)求证:
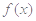 为奇函数;
为奇函数;(2)若
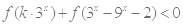 对任意
对任意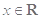 恒成立,求实数
恒成立,求实数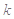 的取值范围.
的取值范围.(1)证明见试题解析;(2)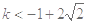 .
.
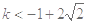 .
.试题分析:(1)这是抽象函数问题,要证明它是奇函数,当然要根据奇函数的定义,证明
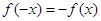 或
或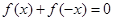 ,由此在已知式
,由此在已知式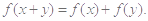 里设
里设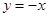 ,从而有
,从而有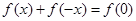 ,因此我们还要先求出
,因此我们还要先求出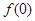 ,这个只要设
,这个只要设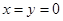 或者有一个为0即可得
或者有一个为0即可得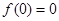 ,故可证得
,故可证得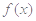 为奇函数;(2)不等式
为奇函数;(2)不等式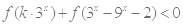 可以利用
可以利用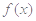 为奇函数的结论,变形为
为奇函数的结论,变形为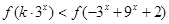 ,再利用函数的单调性去掉符号“
,再利用函数的单调性去掉符号“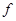 ”,转化为关于
”,转化为关于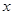 的不等式恒成立问题,即
的不等式恒成立问题,即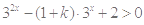 对任意
对任意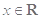 成立,这时还需要用换元法(设
成立,这时还需要用换元法(设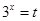 )变化二次不等式怛成立,当然不要忘记
)变化二次不等式怛成立,当然不要忘记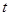 的取值范围.
的取值范围.试题解析:(Ⅰ)证明:∵
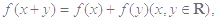 ①
①令
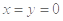 ,代入①式,得
,代入①式,得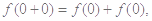 即
即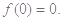
令
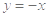 ,代入①式,得
,代入①式,得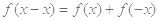 ,又
,又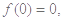
则有
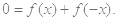 即
即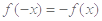 对任意
对任意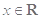 成立,
成立,所以
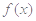 是奇函数. 4分
是奇函数. 4分(Ⅱ)解:
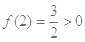 ,即
,即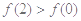 ,又
,又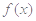 在
在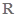 上是单调函数,
上是单调函数,所以
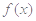 在
在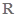 上是增函数.
上是增函数.又由(1)
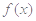 是奇函数.
是奇函数.
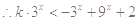 ,即
,即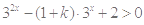 对任意
对任意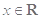 成立.
成立.令
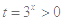 ,问题等价于
,问题等价于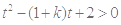 对任意
对任意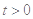 恒成立. 8分
恒成立. 8分令
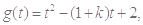 其对称轴
其对称轴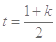 .
.当
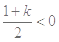 时,即
时,即 时,
时,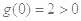 ,符合题意; 10分
,符合题意; 10分当
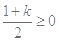 时,对任意
时,对任意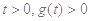 恒成立
恒成立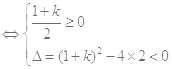
解得
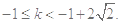 12分
12分综上所述,
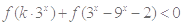 对任意
对任意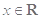 恒成立时,
恒成立时,实数
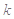 的取值范围是:
的取值范围是: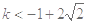 . 13分
. 13分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
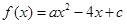 ,且
,且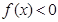 的解集是(1,5).
的解集是(1,5).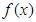 在
在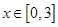 上的值域.
上的值域. 毫克)与时间
毫克)与时间 (小时)成正比;药物释放完毕后,
(小时)成正比;药物释放完毕后, 的函数关系式为
的函数关系式为 (
( 为常数),如图所示,根据图中提供的信息,回答下列问题:
为常数),如图所示,根据图中提供的信息,回答下列问题:
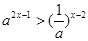
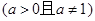 .
.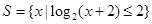 ,集合
,集合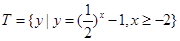 ,求
,求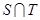 ,
,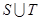 .
.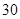 天内每件的销售价格
天内每件的销售价格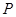 (元)与时间
(元)与时间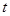 (天)的函数关系是
(天)的函数关系是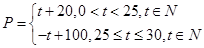 该商品的日销售量
该商品的日销售量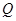 (件)与时间
(件)与时间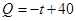
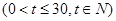 ,设商品的日销售额为
,设商品的日销售额为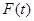 (销售量与价格之积)
(销售量与价格之积) ,若
,若 且
且 ,则
,则 的取值范围_____.
的取值范围_____.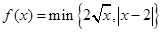 ,其中
,其中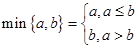 ,若动直线
,若动直线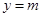 与函数
与函数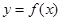 的图像有三个不同的交点,它们的横坐标分别为
的图像有三个不同的交点,它们的横坐标分别为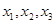 ,则
,则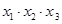 的最大值为( )
的最大值为( )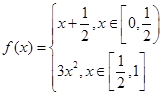 ,若存在
,若存在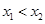 ,使得
,使得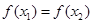 ,则
,则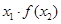 的取值范围为( )
的取值范围为( )
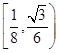

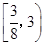
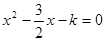 在(-1,1)上有实根,则
在(-1,1)上有实根,则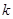 的取值范围为( )
的取值范围为( )