题目内容

对定义域Df、Dg的函数y=f(x)，y=g(x)，规定：函数h(x)=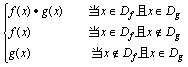

  (1)若函数f(x)=,g(x)=x2，写出函数h(x)的解析式;    (2)求问题(1)中函数h(x)的值域．

 [考场错解]  (1)∵f(x)的定义域Df为(-∞，1)∪(1，+∞)，g(x)的定义域Dg为R.

∴h(x)=

(2)当x≠1时，h(x)==x-1++2≥4．或h(x)= ∈(-∞，0)∪(0，+∞)． ∴h(x)的值域为(4，+∞)，当x=1时，h(x)=1．综合，得h(x)的值域为{1}∪[4，+∞]．

    [专家把脉]  以上解答有两处错误：一是当x∈Df但xDg时，应是空集而不是x≠1．二是求h(x)的值域时，由x≠1求h(x)=x-1++2的值域应分x>1和x<1两种情况的讨论．

[对症下药]  (1)∵f(x)的定义域Df=(-∞，1)∪(1，+∞)·g(x)的定义域是Dg=(-∞，+∞)．所以，h(x)=

 

 

 

 

 

练习册系列答案
相关题目
对定义域是Df．Dg的函数y=f（x）．y=g（x），
规定：函数h（x）=
f(x)g(x)，当x∈Df且x∈Dg
f(x)，当x∈Df且x∉Dg
g(x)，当x∉Df且x∈Dg
．
（1）若函数f（x）=
1
x-1
，g（x）=x2，写出函数h（x）的解析式；
（2）求问题（1）中函数h（x）的值域；
（3）若g（x）=f（x+α），其中α是常数，且α∈[0，π]，请设计一个定义域为R的函数y=f（x），及一个α的值，使得h（x）=cos4x，并予以证明．
对定义域分别是Df、Dg的函数y=f（x）、y=g（x），规定：函数h(x)=
f(x)•g(x)  当x∈Df且x∈Dg
f(x)          当x∈Df且x∉Dg
g(x)          当x∉Df且x∈Dg
．
（1）若函数f(x)=
1
x
，g（x）=x2+4，写出函数h（x）的解析式；
（2）求问题（1）中函数h（x）的值域．
对定义域分别是Df、Dg的函数y=f（x），y=g（x），规定：函数h（x）=
f(x)•g(x)    当x∈Df且x∈Dg
1      当x∈Df且x∉Dg
-1   当x∉Df且x∈Dg
．
（1）若f（α）=sinα•cosα，g（α）=cscα，写出h（α）的解析式；
（2）写出问题（1）中h（α）的取值范围；
（3）若g（x）=f（x+α），其中α是常数，且α∈[0，π]，请设计一个定义域为R的函数y=f（x），及一个α的值，使得h（x）=cos4x，并予以证明．
对定义域分别为Df、Dg的函数y=f（x）、y=g（x），规定：函数h(x)=
f(x)•g(x)(x∈Df且x∈Dg)
f(x)(x∈Df且x∉Dg)
g(x)(x∉Df且x∈Dg).

（1）若函数f(x)=
1
x-1
，g（x）=x2，写出函数h（x）的解析式；
（2）求（1）问中函数h（x）的值域．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网