题目内容
设数列{an}前n的项和为 Sn,且(3-m)Sn+2man=m+3(n∈N*).其中m为常数,m≠-3且m≠0
(1)求证:{an}是等比数列;
(2)若数列{an}的公比满足q=f(m)且b1=a1,bn=
f(bn-1)(n∈N*,n≥2),求证{
}为等差数列,并求bn.
(1)求证:{an}是等比数列;
(2)若数列{an}的公比满足q=f(m)且b1=a1,bn=
| 3 |
| 2 |
| 1 |
| bn |
(1)由(3-m)Sn+2man=m+3,得(3-m)Sn+1+2man+1=m+3,
两式相减,得(3+m)an+1=2man,(m≠-3)
∴
=
,
∴{an}是等比数列.
两式相减,得(3+m)an+1=2man,(m≠-3)
∴
| an+1 |
| an |
| 2m |
| m+3 |
∴{an}是等比数列.
|

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 为等差数列,并求bn.
为等差数列,并求bn.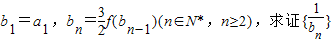 为等差数列,并求bn.
为等差数列,并求bn.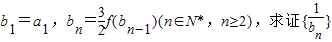 为等差数列,并求bn.
为等差数列,并求bn.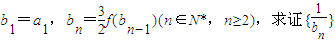 为等差数列,并求bn.
为等差数列,并求bn.