题目内容
设函数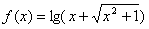 ,
,
(1)确定函数f(x)的定义域;
(2)判断函数f(x)的奇偶性;
(3)证明函数f(x)在其定义域上是单调增函数;
(4)求函数f(x)的反函数。
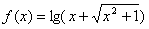 ,
,(1)确定函数f(x)的定义域;
(2)判断函数f(x)的奇偶性;
(3)证明函数f(x)在其定义域上是单调增函数;
(4)求函数f(x)的反函数。
解:(1)由 ,得x∈R,∴定义域为R。
,得x∈R,∴定义域为R。
(2)f(x)是奇函数;
(3)设x1,x2∈R,且x1<x2,则 ,
,
令 ,
,
则



∵x1-x2<0, ,
, ,
, ,
,
∴t1-t2<0,
∴0<t1<t2,∴ ,
,
∴f(x1)-f(x2)<lg1=0,
即f(x1)<f(x2),
∴函数f(x)在R上是单调增函数。
(4)反函数为 (x∈R)。
(x∈R)。
 ,得x∈R,∴定义域为R。
,得x∈R,∴定义域为R。(2)f(x)是奇函数;
(3)设x1,x2∈R,且x1<x2,则
 ,
,令
 ,
,则




∵x1-x2<0,
 ,
, ,
, ,
,∴t1-t2<0,
∴0<t1<t2,∴
 ,
,∴f(x1)-f(x2)<lg1=0,
即f(x1)<f(x2),
∴函数f(x)在R上是单调增函数。
(4)反函数为
 (x∈R)。
(x∈R)。
练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
 的定义域为D,若对于任意
的定义域为D,若对于任意
 ,当
,当 时,都有
时,都有 ,则称函
,则称函 ; ②
; ② ; ③
; ③ .
. 等于( )
等于( ) B.
B. C.
C. D.无法确定
D.无法确定 ,若由函数f(x)确定的数列{an}的自反数列为{bn},求an;
,若由函数f(x)确定的数列{an}的自反数列为{bn},求an; (cn+
(cn+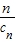 ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论; ,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.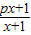 ,若由函数f(x)确定的数列{an}的自反数列为{bn},求an;
,若由函数f(x)确定的数列{an}的自反数列为{bn},求an; (cn+
(cn+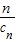 ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论;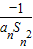 ,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围. ,若由函数f(x)确定的数列{an}的自反数列为{bn},求an;
,若由函数f(x)确定的数列{an}的自反数列为{bn},求an; (cn+
(cn+ ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论; ,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.