题目内容
设数列{an}的前n项和为Sn,已知Sn=2an-2n+1(n∈N*).
(1)求数列{an}的通项公式;
(2)令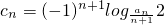 ,数列{cn}的前n项和为Tn,求证:当n∈N*且n≥2时,
,数列{cn}的前n项和为Tn,求证:当n∈N*且n≥2时,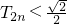 .
.
解:(1)由Sn=2an-2n+1,得Sn-1=2an-1-2n(n≥2).
两式相减,得an=2an-2an-1-2n,即an-2an-1=2n(n≥2).
于是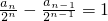 ,所以数列
,所以数列 是公差为1的等差数列.(5分)
是公差为1的等差数列.(5分)
又S1=2a1-22,所以a1=4.
所以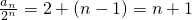 ,故an=(n+1)•2n.(6分)
,故an=(n+1)•2n.(6分)
(2)因为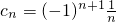 ,则当n≥2时,
,则当n≥2时, =
= =
= .(9分)
.(9分)
下面证
令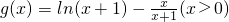 ,则
,则 ,
,
∴g(x)在(0,+∞)时单调递增,g(x)>g(0)=0,即当x>0时,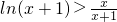
令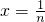 ,
,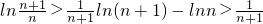 ,
,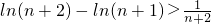 ,
,
,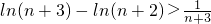 ,,
,,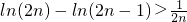
以上n个式相加,即有
∴ (14分)
(14分)
分析:(1)由Sn=2an-2n+1,得Sn-1=2an-1-2n(n≥2).两式相减,得an=2an-2an-1-2n,即an-2an-1=2n(n≥2).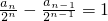 ,所以数列
,所以数列 是公差为1的等差数列.由此可知an=(n+1)•2n.
是公差为1的等差数列.由此可知an=(n+1)•2n.
(2)由题意知 =
= =
= .然后再证明证
.然后再证明证 .
.
点评:本题考查数列性质的综合运用,解题时要认真审题,注意公式的灵活运用.
两式相减,得an=2an-2an-1-2n,即an-2an-1=2n(n≥2).
于是
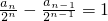 ,所以数列
,所以数列 是公差为1的等差数列.(5分)
是公差为1的等差数列.(5分)又S1=2a1-22,所以a1=4.
所以
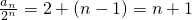 ,故an=(n+1)•2n.(6分)
,故an=(n+1)•2n.(6分)(2)因为
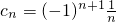 ,则当n≥2时,
,则当n≥2时, =
= =
= .(9分)
.(9分)下面证

令
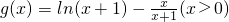 ,则
,则 ,
,∴g(x)在(0,+∞)时单调递增,g(x)>g(0)=0,即当x>0时,
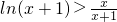
令
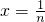 ,
,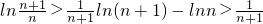 ,
,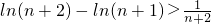 ,
,,
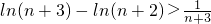 ,,
,,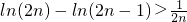
以上n个式相加,即有

∴
 (14分)
(14分)分析:(1)由Sn=2an-2n+1,得Sn-1=2an-1-2n(n≥2).两式相减,得an=2an-2an-1-2n,即an-2an-1=2n(n≥2).
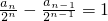 ,所以数列
,所以数列 是公差为1的等差数列.由此可知an=(n+1)•2n.
是公差为1的等差数列.由此可知an=(n+1)•2n.(2)由题意知
 =
= =
= .然后再证明证
.然后再证明证 .
.点评:本题考查数列性质的综合运用,解题时要认真审题,注意公式的灵活运用.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目