题目内容
已知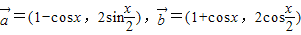 ,设
,设
(1)若函数f(x)和函数g(x)的图象关于原点对称,求函数g(x)的解析式;
(2)若h(x)=g(x)-λf(x)+1在
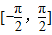 上是增函数,求实数λ的取值范围.
上是增函数,求实数λ的取值范围.
【答案】分析:(1)利用向量的坐标运算与三角函数间的关系式可求得f(x)=sin2x+2sinx,由f(x)和函数g(x)的图象关于原点对称,可求得函数g(x)的解析式;
(2)依题意可求得h(x)的解析式,利用h′(x)≥0在[-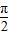 ,
,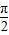 ]恒成立即可求得实数λ的取值范围.
]恒成立即可求得实数λ的取值范围.
解答:解:(1)∵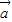 -
-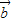 =(-2cosx,2sin
=(-2cosx,2sin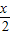 -2cos
-2cos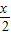 ),|
),|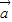 -
-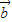 |=4cos2x+
|=4cos2x+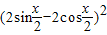 =4cos2x+4-4sinx,
=4cos2x+4-4sinx,
∴f(x)=2+sinx-cos2x-1+sinx=sin2x+2sinx…(3分)
设(x,y)为g(x)图象上任意一点,则(-x,-y)为f(x)图象上的点,
∴-y=sin2(-x)+2sin(-x)=sin2x-2sinx,
∴y=-sin2x+2sinx即g(x)=-sin2x+2sinx…(6分)
(2)h(x)=-sin2x+2sinx-λ(sin2x+2sinx)+1
=(-1-λ)sin2x+(2-2λ)sinx+1,…(8分)
h'(x)=-2(1+λ)sinxcosx+(2-2λ)cosx,
∵h(x)在[-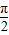 ,
,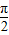 ]上是增函数
]上是增函数
∴h′(x)≥0在[-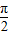 ,
,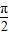 ]恒成立,
]恒成立,
即-2(1+λ)sinxcosx+(2-2λ)cosx≥0,当x=±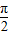 时,不等式恒成立
时,不等式恒成立
当x∈(-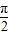 ,
,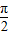 )时,cosx>0,
)时,cosx>0,
∴-2(1+λ)sinx+2-2λ≥0即λ≤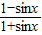 =-1+
=-1+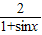 ,…(10分)
,…(10分)
∵sinx∈(-1,1)
∴-1+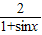 ∈(0,+∞),
∈(0,+∞),
∴λ≤0 …(12分)
点评:本题考查向量的坐标运算与三角函数间的关系式,考查三角函数的最值,考查导数在研究函数单调性与最值中的应用,综合性强,难度大,属于难题.
(2)依题意可求得h(x)的解析式,利用h′(x)≥0在[-
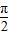 ,
,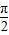 ]恒成立即可求得实数λ的取值范围.
]恒成立即可求得实数λ的取值范围.解答:解:(1)∵
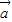 -
-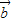 =(-2cosx,2sin
=(-2cosx,2sin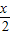 -2cos
-2cos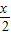 ),|
),|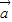 -
-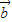 |=4cos2x+
|=4cos2x+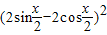 =4cos2x+4-4sinx,
=4cos2x+4-4sinx,∴f(x)=2+sinx-cos2x-1+sinx=sin2x+2sinx…(3分)
设(x,y)为g(x)图象上任意一点,则(-x,-y)为f(x)图象上的点,
∴-y=sin2(-x)+2sin(-x)=sin2x-2sinx,
∴y=-sin2x+2sinx即g(x)=-sin2x+2sinx…(6分)
(2)h(x)=-sin2x+2sinx-λ(sin2x+2sinx)+1
=(-1-λ)sin2x+(2-2λ)sinx+1,…(8分)
h'(x)=-2(1+λ)sinxcosx+(2-2λ)cosx,
∵h(x)在[-
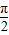 ,
,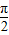 ]上是增函数
]上是增函数∴h′(x)≥0在[-
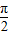 ,
,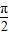 ]恒成立,
]恒成立,即-2(1+λ)sinxcosx+(2-2λ)cosx≥0,当x=±
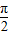 时,不等式恒成立
时,不等式恒成立当x∈(-
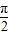 ,
,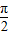 )时,cosx>0,
)时,cosx>0,∴-2(1+λ)sinx+2-2λ≥0即λ≤
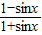 =-1+
=-1+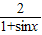 ,…(10分)
,…(10分)∵sinx∈(-1,1)
∴-1+
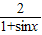 ∈(0,+∞),
∈(0,+∞),∴λ≤0 …(12分)
点评:本题考查向量的坐标运算与三角函数间的关系式,考查三角函数的最值,考查导数在研究函数单调性与最值中的应用,综合性强,难度大,属于难题.

练习册系列答案
相关题目
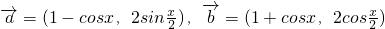 ,设
,设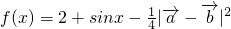
 上是增函数,求实数λ的取值范围.
上是增函数,求实数λ的取值范围.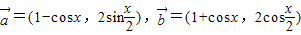 ,设
,设
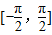 上是增函数,求实数λ的取值范围.
上是增函数,求实数λ的取值范围.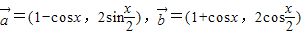 ,设
,设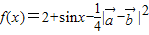
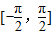 上是增函数,求实数λ的取值范围.
上是增函数,求实数λ的取值范围.