题目内容
将函数y=f(x)·sinx的图象向右平移
个单位后，再作关于x轴的对称变换，得到y=1-2sin2x的图象，则f(x)可以是（ ）A.cosx B.2cosx C.sinx D.2sinx
解法一:将y=1-2sin2x=cos2x作关于x轴的对称变换，得y=-cos2x,然后向左平移个单位，得y=-cos2(x+
)=sin2x=f(x)·sinx,
∴f(x)=2cosx.
解法二：把y=f(x)·sinx向右平移
个单位后，得到y1=f(x-
)·sin(x-
),再作关于x轴的对称变换后，得到y2=-f(x-
)sin(x-
).
由题意，得-f(x-
)sin(x-
).
∵1-2sin2x=cos2x=sin(
-2x)
=2sin(
-x)cos(
-x),
∴-f(x-
)sin(x-
)
=2sin(
-x)cos(
-x).
∴f(x-
)=2cos(
-x)
=2cos(x-
).
∴f(x)=2cosx.
答案:B
练习册系列答案
相关题目
个单位，得到的曲线与y=
sinx的图象相同，则y=f(x)的函数表达式为（ ）
sin(
x-
) B.y=
sin2(x+
)
sin(
x+
) D.y=
sin(2x-
)
,2)平移后，得到函数y=3-2sin2x的图象，则f(x)是（ ） 
个单位后再作关于x轴对称的曲线，得到函数y=1-2sin2x的图象，则f(x)是( )
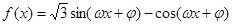
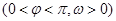为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为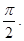
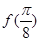的值；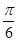
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍，纵坐标不变，得到函数y=g(x)的图象,求g(x)的单调递减区间.