题目内容
 设奇函数f(x)的定义域为[-5,5],若当x∈[0,5]时,f(x)的图象如图,则不等式f(x)<0的解是
设奇函数f(x)的定义域为[-5,5],若当x∈[0,5]时,f(x)的图象如图,则不等式f(x)<0的解是(2,5]∪(-2,0)
(2,5]∪(-2,0)
,在R上的零点的个数是3
3
个.分析:本题是一个研究奇函数对称性及函数图象的位置与函数值符号对应关系的题,可先补全函数在定义域上的图象,再由图象观察出不等式的解集,给出正确答案.
解答: 解:由于奇函数关于原点对称,故函数(x)在定义域为[-5,5]的图象如右图
解:由于奇函数关于原点对称,故函数(x)在定义域为[-5,5]的图象如右图
由图象知不等式f(x)<0的解集是(2,5]∪(-2,0),
在R上的零点的个数是 3个
故答案为:(2,5]∪(-2,0);3.
 解:由于奇函数关于原点对称,故函数(x)在定义域为[-5,5]的图象如右图
解:由于奇函数关于原点对称,故函数(x)在定义域为[-5,5]的图象如右图由图象知不等式f(x)<0的解集是(2,5]∪(-2,0),
在R上的零点的个数是 3个
故答案为:(2,5]∪(-2,0);3.
点评:本题考查函数的图象,解题的关键是理解函数图象的数字特征,本题的重点是利用函数的图象解不等式,难点是根据函数的奇函数的性质作出对称区间上的函数的图象来,对函数图象的考查是新教材实验区高考考试的热点,近几年明显加强了对图形的考查,学习时要注意归纳此类题的解题规律

练习册系列答案
相关题目
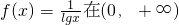 是减函数;
是减函数;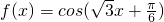 ,则f(x)+f'(x)是奇函数;
,则f(x)+f'(x)是奇函数;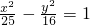 的一个焦点到渐近线的距离是5;
的一个焦点到渐近线的距离是5; 是减函数;
是减函数; ,则f(x)+f'(x)是奇函数;
,则f(x)+f'(x)是奇函数; 的一个焦点到渐近线的距离是5;
的一个焦点到渐近线的距离是5;