题目内容
 一个几何体的三视图如图所示,则此几何体的表面积为
一个几何体的三视图如图所示,则此几何体的表面积为
| ||
| 2 |
| ||
| 2 |
分析:由几何体的俯视图是半圆,主视图是等腰三角形,且左视图是直角三角形得到原几何体是半圆锥,然后根据图中给出的量求半圆锥的表面积.
解答: 解:由几何体的三视图可得其原图形是底面半径为1,高为2的半圆锥,如图,该几何体的表面积等于下底半圆面的面积加上等腰三角形PAB的面积加上以1为底面半径,以2为高的圆锥侧面积的一半.
解:由几何体的三视图可得其原图形是底面半径为1,高为2的半圆锥,如图,该几何体的表面积等于下底半圆面的面积加上等腰三角形PAB的面积加上以1为底面半径,以2为高的圆锥侧面积的一半.
底面半圆面积为
π,
三角形PAB的面积为
×2×2=2,
因为圆锥的底面半径为1,高为2,所以母线长为
,
所以圆锥侧面积的一半为
×
×2π×
=
.
所以该几何体的表面积为
+
+2=
π+2.
故答案为
π+2.
 解:由几何体的三视图可得其原图形是底面半径为1,高为2的半圆锥,如图,该几何体的表面积等于下底半圆面的面积加上等腰三角形PAB的面积加上以1为底面半径,以2为高的圆锥侧面积的一半.
解:由几何体的三视图可得其原图形是底面半径为1,高为2的半圆锥,如图,该几何体的表面积等于下底半圆面的面积加上等腰三角形PAB的面积加上以1为底面半径,以2为高的圆锥侧面积的一半.底面半圆面积为
| 1 |
| 2 |
三角形PAB的面积为
| 1 |
| 2 |
因为圆锥的底面半径为1,高为2,所以母线长为
| 5 |
所以圆锥侧面积的一半为
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| ||
| 2 |
所以该几何体的表面积为
| ||
| 2 |
| π |
| 2 |
| ||
| 2 |
故答案为
| ||
| 2 |
点评:本题考查了由三视图求表面积,解答此题的关键是还原原几何体,由三视图还原原几何体首先看俯视图,结合主视图和左视图得原几何体,此题属中低档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
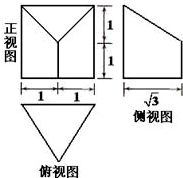
 (2013•房山区二模)一个几何体的三视图如图所示,则这个几何体的表面积为( )
(2013•房山区二模)一个几何体的三视图如图所示,则这个几何体的表面积为( )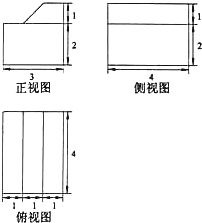 (2012•天津)一个几何体的三视图如图所示(单位:m),则该几何体的体积为
(2012•天津)一个几何体的三视图如图所示(单位:m),则该几何体的体积为 一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的表面积为
一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的表面积为 (2010•河东区一模)一个几何体的三视图如图所示,则该几何体(不考虑接触点)的表面积为
(2010•河东区一模)一个几何体的三视图如图所示,则该几何体(不考虑接触点)的表面积为