��Ŀ����
����Ŀ����УΪ���С������˶�һСʱ������ƻ���һ��ֱ��������ABC�Ŀյ�����һ��ռ�����ΪS��ƽ���ף��ľ���AMPN�������أ���ͼ����M��AC�ϣ���N��AB�ϣ���P����б��BC�ϣ���֪��ACB=60�㣬|AC|=30�ף�|AM|=x�ף�x��[10��20]�������AMPN��������ÿƽ�������Ϊ ![]() Ԫ���ٰѾ���AMPN���⣨��Ӱ���֣����ϲ�ƺ��ÿƽ�������Ϊ
Ԫ���ٰѾ���AMPN���⣨��Ӱ���֣����ϲ�ƺ��ÿƽ�������Ϊ ![]() Ԫ��kΪ����������
Ԫ��kΪ����������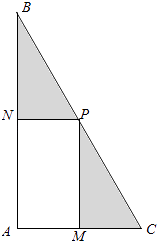
��1������x��ʾS������S��ȡֵ��Χ��
��2���������T�������S���T=f��S����
��3�����ѡȡ|AM|��ʹ�����T��ͣ���Ҫ����������ۣ���
���𰸡�
��1���⣺��Rt��PMC�У���Ȼ|MC|=30��x����PCM=60�㣬
�� ![]() ��
��
����AMPN����� ![]() ��x��[10��20]��
��x��[10��20]��
��x��30��x���ܣ� ![]() ��2=225����x=15ʱ���ɵ����ֵΪ225
��2=225����x=15ʱ���ɵ����ֵΪ225 ![]() ��
��
��x=10��20ʱ��ȡ����Сֵ200 ![]() ��
��
���� ![]() ����
����
��2���⣺����AMPN�����������T1= ![]() ��
��
�֡�ABC�����Ϊ ![]() ������ƺ���T2=
������ƺ���T2= ![]() ��
��
�������T=T1+T2��
�� ![]() ��
�� ![]()
��3���⣺�� ![]() ��
��
���ҽ��� ![]() ��
�� ![]() ʱ�Ⱥų�����
ʱ�Ⱥų�����
��ʱ ![]() �����x=12��x=18��
�����x=12��x=18��
��ѡȡ|AM|�ij�Ϊ12��18��ʱ�����T���
����������1���������⣬�õ��������ص�������ٽ�Ͼ��ε�������㹫ʽ���������ɶ��κ�����������÷�Χ����2���������ε����������õ�����ۣ��õ���Χ����3��ʹ�þ�ֵ����ʽ�õ�������ʱ��x=12��x=18.
�����㾫�������պ�������ֵ���伸������ͺ�����ֵ�ǽ����ĸ�������Ҫ֪�����ö��κ��������ʣ��䷽�������������С��ֵ������ͼ�����������С��ֵ�����ú��������Ե��жϺ��������С��ֵ������ֵ�������䷽��(���λ��Ĵ�)���ڡ��б�ʽ�������۷����������ܻ�Ԫ�����ݲ���ʽ���������ĵ����Է���

 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�����Ŀ��ij����2007����2013��ũ������ͥ�˾�������y����λ��ǧԪ�������������
��� | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
��ݴ���t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
�˾�������y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
������y����t�����Իع鷽�̣�
�������ã����еĻع鷽�̣�����2007����2013��õ���ũ������ͥ�˾�������ı仯�������Ԥ��õ���2015��ũ������ͥ�˾������룮
�����ع�ֱ�ߵ�б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ�� ![]() =
= 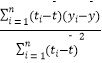 ��
�� ![]() =
= ![]() ��
�� ![]()
![]() ��
��

