题目内容
已知函数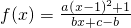 (a、b、c∈N)的图象按向量
(a、b、c∈N)的图象按向量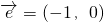 平移后得到的图象关于原点对称,且f(2)=2,f(3)<3.
平移后得到的图象关于原点对称,且f(2)=2,f(3)<3.
(Ⅰ)求a,b,c的值;
(Ⅱ)设x是正实数,求证:[f(x+1)]n-f(xn+1)≥2n-2.
(Ⅰ)解:函数f(x)的图象按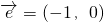 平移后得到的图象所对应的函数式为
平移后得到的图象所对应的函数式为 .
.
∵函数f(x)的图象平移后得到的图象关于原点对称,
∴f(-x+1)=-f(x+1),即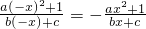 .
.
∵a∈N,∴ax2+1>0.∴-bx+c=-bx-c,∴c=0.
又∵f(2)=2,∴ .∴a+1=2b,∴a=2b-1. ①
.∴a+1=2b,∴a=2b-1. ①
又 .∴4a+1<6b. ②
.∴4a+1<6b. ②
由①,②及a、b∈N,得a=1,b=1.
(Ⅱ)证明:n=1时,结论显然成立.
当n≥2时,
=
 =
= =
=
 .
.
分析:(Ⅰ)利用平移规律,可得 ,根据函数f(x)的图象平移后得到的图象关于原点对称,可得f(-x+1)=-f(x+1),从而可求c的值,根据f(2)=2,f(3)<3,a、b∈N,可得a,b的值;
,根据函数f(x)的图象平移后得到的图象关于原点对称,可得f(-x+1)=-f(x+1),从而可求c的值,根据f(2)=2,f(3)<3,a、b∈N,可得a,b的值;
(Ⅱ)当n≥2时,利用二项展开式,再进行放缩,即可证得结论.
点评:本题考查函数解析式的确定,考查不等式的证明,考查函数的性质,同时考查二项式定理的运用,属于中档题.
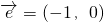 平移后得到的图象所对应的函数式为
平移后得到的图象所对应的函数式为 .
.∵函数f(x)的图象平移后得到的图象关于原点对称,
∴f(-x+1)=-f(x+1),即
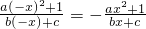 .
.∵a∈N,∴ax2+1>0.∴-bx+c=-bx-c,∴c=0.
又∵f(2)=2,∴
 .∴a+1=2b,∴a=2b-1. ①
.∴a+1=2b,∴a=2b-1. ①又
 .∴4a+1<6b. ②
.∴4a+1<6b. ②由①,②及a、b∈N,得a=1,b=1.
(Ⅱ)证明:n=1时,结论显然成立.
当n≥2时,

=

 =
= =
=
 .
.分析:(Ⅰ)利用平移规律,可得
 ,根据函数f(x)的图象平移后得到的图象关于原点对称,可得f(-x+1)=-f(x+1),从而可求c的值,根据f(2)=2,f(3)<3,a、b∈N,可得a,b的值;
,根据函数f(x)的图象平移后得到的图象关于原点对称,可得f(-x+1)=-f(x+1),从而可求c的值,根据f(2)=2,f(3)<3,a、b∈N,可得a,b的值;(Ⅱ)当n≥2时,利用二项展开式,再进行放缩,即可证得结论.
点评:本题考查函数解析式的确定,考查不等式的证明,考查函数的性质,同时考查二项式定理的运用,属于中档题.

练习册系列答案
相关题目
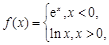 则
则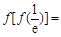 ( )
( )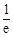 B.
B.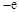 C.
C.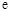 D.
D. (a,b,c∈N),且f(2)=2,f(3)<3,
(a,b,c∈N),且f(2)=2,f(3)<3,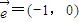 平移后得到的图象关于原点对称.
平移后得到的图象关于原点对称.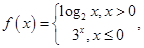 则
则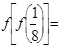 ( )
( )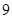 B.
B.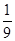 C.
C.
 D.
D.
 已知函数
已知函数  若
若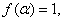
 =
=