题目内容
设a,b,c为实数,f(x)=(x+a)(x2+bx+c),g(x)=(ax+1)(cx2+bx+1).
记集合S={x|f(x)=0,x∈R},T={x|g(x)=0,x∈R}.若|S|,|T|分别为集合S,T的元素个
数,则下列结论不可能的是( )
记集合S={x|f(x)=0,x∈R},T={x|g(x)=0,x∈R}.若|S|,|T|分别为集合S,T的元素个
数,则下列结论不可能的是( )
| A.|S|=1且|T|=0 | B.|S|=1且|T|=1 |
| C.|S|=2且|T|=2 | D.|S|=2且|T|=3 |
D
本台考查分类讨论思想以及推理能力。
显然方程 、
、 的实根根数相同,可以为0,1,2个,故当
的实根根数相同,可以为0,1,2个,故当 时,|S|=1,2,3,与其对应的|T|=0,1,2;当
时,|S|=1,2,3,与其对应的|T|=0,1,2;当 时,|S|=1,2,3,与其对应的|T|=1,2,3.对照选项检验可知选D。
时,|S|=1,2,3,与其对应的|T|=1,2,3.对照选项检验可知选D。
显然方程
 、
、 的实根根数相同,可以为0,1,2个,故当
的实根根数相同,可以为0,1,2个,故当 时,|S|=1,2,3,与其对应的|T|=0,1,2;当
时,|S|=1,2,3,与其对应的|T|=0,1,2;当 时,|S|=1,2,3,与其对应的|T|=1,2,3.对照选项检验可知选D。
时,|S|=1,2,3,与其对应的|T|=1,2,3.对照选项检验可知选D。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 )∩(
)∩( )等于( )
)等于( )
 ,则
,则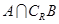 等( )
等( )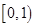
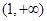
 ,集合
,集合 ,则集合
,则集合 =( )
=( )



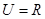 ,集合
,集合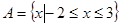 ,
,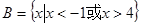 ,那么集合
,那么集合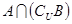 等于
等于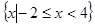
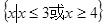

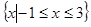
 ,若
,若 ,则
,则 ( )
( )


 ,
,
 ,
, ,则
,则 =( )
=( )



 ,
, ,则
,则 =
= 


