题目内容
直线l到点A(1,1)和B(-2,3)的距离分别是1和2,则符合条件的直线l的条数是
- A.1
- B.2
- C.3
- D.4
D
分析:根据题意,直线l与点A为圆心、半径为1的圆相切,同时又与点B为圆心、半径为2的圆相切,因此找出两个圆的公切线的条数即可.算出两圆的圆心距等于 ,大于两圆的半径之和,得两圆相外离,由此即可得到符合条件的直线l的条数.
,大于两圆的半径之和,得两圆相外离,由此即可得到符合条件的直线l的条数.
解答:∵直线l到点A(1,1)的距离是1,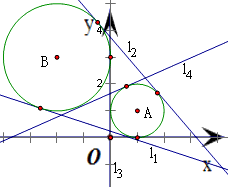
∴直线l与点A为圆心、半径为1的圆相切
同理可得直线l与点B(-2,3)为圆心、半径为2的圆相切
问题转化为圆A与圆B公切线的条数
∵A、B两点的距离为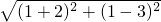 =
= ,且
,且 >2+1=3
>2+1=3
∴圆A与圆B的位置关系是外离
因此,圆A与圆B共有4条公切线
故选:D
点评:本题给出动直线到两个定点的距离分别为1和2,求满足条件的直线的条数,着重考查了平面内两点之间的距离、直线与圆的位置关系和圆与圆的位置关系等知识点,属于中档题.
分析:根据题意,直线l与点A为圆心、半径为1的圆相切,同时又与点B为圆心、半径为2的圆相切,因此找出两个圆的公切线的条数即可.算出两圆的圆心距等于
 ,大于两圆的半径之和,得两圆相外离,由此即可得到符合条件的直线l的条数.
,大于两圆的半径之和,得两圆相外离,由此即可得到符合条件的直线l的条数.解答:∵直线l到点A(1,1)的距离是1,

∴直线l与点A为圆心、半径为1的圆相切
同理可得直线l与点B(-2,3)为圆心、半径为2的圆相切
问题转化为圆A与圆B公切线的条数
∵A、B两点的距离为
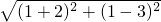 =
= ,且
,且 >2+1=3
>2+1=3∴圆A与圆B的位置关系是外离
因此,圆A与圆B共有4条公切线
故选:D
点评:本题给出动直线到两个定点的距离分别为1和2,求满足条件的直线的条数,着重考查了平面内两点之间的距离、直线与圆的位置关系和圆与圆的位置关系等知识点,属于中档题.

练习册系列答案
相关题目
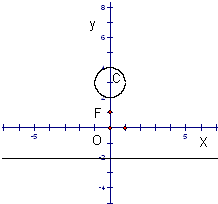 如图,已知点F(0,1),直线L:y=-2,及圆C:x2+(y-3)2=1.
如图,已知点F(0,1),直线L:y=-2,及圆C:x2+(y-3)2=1.