题目内容
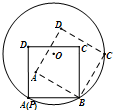 设圆O的半径为2,点P为圆周上给定一点,如图所示,放置边长为2的正方形ABCD(实线所示,正方形的顶点A与点P重合,点B在圆周上).现将正方形ABCD沿圆周按顺时针方向连续滚动,当点A首次回到点P的位置时,点A所走过的路径的长度为( )
设圆O的半径为2,点P为圆周上给定一点,如图所示,放置边长为2的正方形ABCD(实线所示,正方形的顶点A与点P重合,点B在圆周上).现将正方形ABCD沿圆周按顺时针方向连续滚动,当点A首次回到点P的位置时,点A所走过的路径的长度为( )| A、4π | ||||
B、(3+
| ||||
C、(1+2
| ||||
D、(2+
|
分析:根据题意可画出正方形旋转的过程中顶点落在圆上的次序,由图易得当点A首次回到点P的位置时,正方形滚动了3圈共12次,计算每次的路程,求和即可.
解答:解: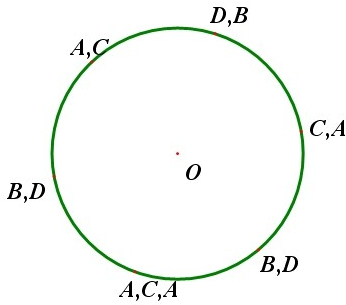 ∵圆O的半径r=2,正方形ABCD的边长a=2,
∵圆O的半径r=2,正方形ABCD的边长a=2,
∴以正方形的边为弦时所对的圆心角为
,
正方形在圆上滚动时点的顺序依次为如图所示,
∴当点A首次回到点P的位置时,正方形滚动了3圈共12次,
设第i次滚动,点A的路程为Ai,
则A1=
×|AB|=
,
A2=
×|AC|=
,
A3=
×|DA|=
,
A4=0,
∴点A所走过的路径的长度为3(A1+A2+A3+A4)=(2+
)π.
故选:D.
 ∵圆O的半径r=2,正方形ABCD的边长a=2,
∵圆O的半径r=2,正方形ABCD的边长a=2,∴以正方形的边为弦时所对的圆心角为
| π |
| 3 |
正方形在圆上滚动时点的顺序依次为如图所示,
∴当点A首次回到点P的位置时,正方形滚动了3圈共12次,
设第i次滚动,点A的路程为Ai,
则A1=
| π |
| 6 |
| π |
| 3 |
A2=
| π |
| 6 |
2
| ||
| 6 |
A3=
| π |
| 6 |
| π |
| 3 |
A4=0,
∴点A所走过的路径的长度为3(A1+A2+A3+A4)=(2+
| 2 |
故选:D.
点评:本题考查了圆的性质的灵活应用,和弧长公式的应用.以及分析问题数据和处理数据的能力,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 (2012•河南模拟)如图,AB是圆O的直径,以B为圆心的圆B与圆O的一个交点为P.过点A作直线交圆O于点Q,交圆B于点M、N.
(2012•河南模拟)如图,AB是圆O的直径,以B为圆心的圆B与圆O的一个交点为P.过点A作直线交圆O于点Q,交圆B于点M、N.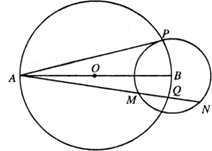
 时,求MN的长.
时,求MN的长.
 时,求MN的长.
时,求MN的长.