题目内容
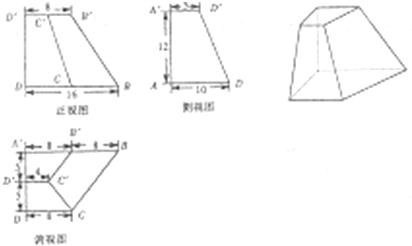 已知棱台ABCD-A′B′C′D′及其三视图尺寸如图所示,P、Q分别为B'B,CB的中点.
已知棱台ABCD-A′B′C′D′及其三视图尺寸如图所示,P、Q分别为B'B,CB的中点.(1)填写棱台各顶点字母,并证明:PQ∥平面AA′D′D;
(2)求二面角B-DD′-A的正切值.
分析:(1)根据翻折前后变与不变标出字母,欲证PQ∥平面A'ADD',根据线面平行的判定定理可知只需PQ与平面A'ADD'内一直线平行即可,连接B'C、PQ,则PQ∥B'C,根据A'B'CD为矩形,则B'C∥A'D,从而PQ∥A'D又PQ?平面A'ADD',A'D?平面A'ADD',满足定理所需条件;
(2)延长DD',AA',BB'交于一点G,作A'H⊥D'D于H,连接HB',根据二面角平面角的定义可知∠B'HA'为二面角B-DD'-A的平面角,在Rt△B'HA'中,求出此角,即可求出二面角B-DD'-A的正切值.
(2)延长DD',AA',BB'交于一点G,作A'H⊥D'D于H,连接HB',根据二面角平面角的定义可知∠B'HA'为二面角B-DD'-A的平面角,在Rt△B'HA'中,求出此角,即可求出二面角B-DD'-A的正切值.
解答: 证明:(1)字母如图所示.(2分)
证明:(1)字母如图所示.(2分)
∵梯形A'ADD'、A'ABB'、A'B'C'D'、ABCD均为直角梯形,
且A′B′=DC=
AB=8,2D'C'=A'B'=DC
连接B'C、PQ,则PQ∥B'C,又∵A'B'∥DC,且A'B'=DC,∴A'B'CD为矩形
∴B'C∥A'D,∴PQ∥A'D又PQ?平面A'ADD',A'D?平面A'ADD'
∴PQ∥平面A'ADD'.(6分)
(2)延长DD',AA',BB'交于一点G,
∵B'A'⊥面ADG,作A'H⊥D'D于H,连接HB',则HB'⊥DD'
则∠B'HA'为二面角B-DD'-A的平面角.(9分)
在Rt△D'A'G中,易得A'G=12,A'D'=5
∴
×A′H×D′G=
×5×12,即A′H=
∴tan∠B′HA′=
=
.即二面角B-DD'-A的正切值为
.(13分)
 证明:(1)字母如图所示.(2分)
证明:(1)字母如图所示.(2分)∵梯形A'ADD'、A'ABB'、A'B'C'D'、ABCD均为直角梯形,
且A′B′=DC=
| 1 |
| 2 |
连接B'C、PQ,则PQ∥B'C,又∵A'B'∥DC,且A'B'=DC,∴A'B'CD为矩形
∴B'C∥A'D,∴PQ∥A'D又PQ?平面A'ADD',A'D?平面A'ADD'
∴PQ∥平面A'ADD'.(6分)
(2)延长DD',AA',BB'交于一点G,
∵B'A'⊥面ADG,作A'H⊥D'D于H,连接HB',则HB'⊥DD'
则∠B'HA'为二面角B-DD'-A的平面角.(9分)
在Rt△D'A'G中,易得A'G=12,A'D'=5
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 60 |
| 13 |
∴tan∠B′HA′=
| A′B′ |
| A′H |
| 26 |
| 15 |
| 26 |
| 15 |
点评:本题主要考查了线面平行的判定,以及二面角的度量,同时考查了空间想象能力、推理能力和计算能力,属于中档题.

练习册系列答案
相关题目
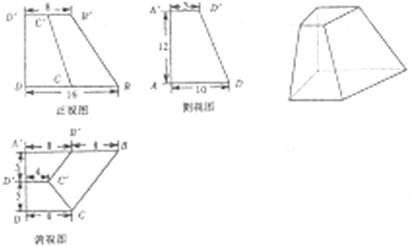 已知棱台ABCD-A′B′C′D′及其三视图尺寸如图所示,P、Q分别为B'B,CB的中点.
已知棱台ABCD-A′B′C′D′及其三视图尺寸如图所示,P、Q分别为B'B,CB的中点.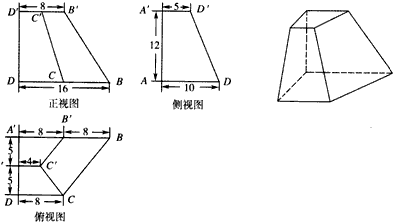
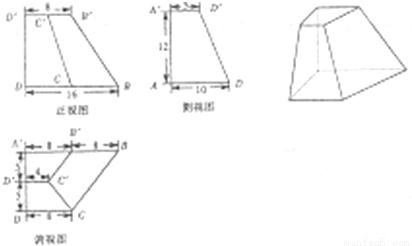 已知棱台ABCD-A′B′C′D′及其三视图尺寸如图所示,P、Q分别为B'B,CB的中点.
已知棱台ABCD-A′B′C′D′及其三视图尺寸如图所示,P、Q分别为B'B,CB的中点.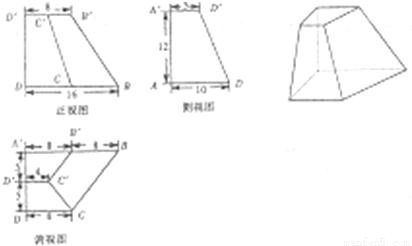 已知棱台ABCD-A′B′C′D′及其三视图尺寸如图所示,P、Q分别为B'B,CB的中点.
已知棱台ABCD-A′B′C′D′及其三视图尺寸如图所示,P、Q分别为B'B,CB的中点.