题目内容
对于函数f(x)，若存在x0∈R，使f(x0)=x0成立，则称x0为f(x)的不动点.已知函数f(x)=ax2+(b+1)x+(b-1)(a≠0).(1)当a=1,b=-2时，求函数f(x)的不动点；
(2)若对任意实数b，函数f(x)恒有两个相异的不动点，求a的取值范围.
解：（1）当a=1,b=-2时，f(x)=x2-x-3.
由题意可知x=x2-x-3，
得x1=-1,x2=3.
故当a=1,b=-2时，f(x)的两个不动点为-1,3.
（2）∵f(x)=ax2+(b+1)x+(b-1)(a≠0)恒有两个不动点，
∴x=ax2+(b+1)x+(b-1),
即ax2+bx+(b-1)=0恒有两个相异的实数根，得Δ=b2-4ab+
于是Δ′=（
解得0＜a＜1.
故当b∈R，f(x)恒有两个相异的不动点时，a的取值范围为0＜a＜1.
练习册系列答案
相关题目
，使
成立，则称x0为f(x)的不动点. 如果函数
有且仅有两个不动点0，2，且
，求证：
；
，
为数列{bn}的前n项和，求证：
已知函数f(x)=ax2+(b+1)x+(b–1)(a≠0)
对称，求b的最小值.
<m<1；
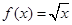的等域区间是 .
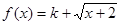是布林函数，则实数k的取值范围是
.