Question

下列说法不正确的是

1. A.
   “?x₀∈R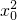，-x₀-1＜0”的否定是“”
2. B.
   命题“若x＞0且y＞0，则x+y＞0”的否命题是假命题
3. C.
   满足x₁＜1＜x₂”和“函数f（x）=log₂（ax-1）在[1，2]上单调递增”同时为真
4. D.
   △ABC中，A是最大角，则＜sin²A是△ABC为钝角三角形的弃要条件

Answer 1

C
分析：逐个选项验证，分别判断它们的正误，其中ABD均正确，选项C的a值不能使两者同时成立，故可得答案．
解答：由特称命题的否定可知选项A正确；
命题“若x＞0且y＞0，则x+y＞0”的逆命题为“若x+y＞0，则x＞0且y＞0”且为假，
故“若x＞0且y＞0，则x+y＞0”的否命题也为假，故选项B正确；
记函数f（x）=2x²+x+a，则方程2x²+x+a=0的两根满足x₁＜1＜x₂，即f（1）＜0，
解得a＜-3，此时f（x）=log₂（ax-1）在[1，2]上单调递增不正确，故选项C错误；
在三角形ABC中，A是最大角，△ABC为钝角三角形的充要条件是b²+c²＜a²，
即＜sin²A，故选项D正确．
故选C
点评：本题考查命题的正误的判断，涉及特称命题的否定，以及命题真假的关系，属基础题．