题目内容
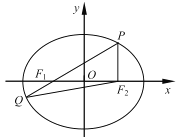
【题目】设抛物线
的焦点为F，准线为l，A为C上一点，已知以F为圆心，FA为半径的圆F交l于M.N点.
（1）若
，
的面积为
，求抛物线方程；
（2）若A.M.F三点在同一直线m上，直线n与m平行，且n与C只有一个公共点，求坐标原点到直线n、m距离的比值.
【答案】（1）
；（2）
【解析】
（1）由抛物线的定义，以及圆的对称性可得
为等边三角形，可由其高线求得边长，进而表达出面积，列方程解得
即可求得抛物线方程.
（2）由A.M.F三点共线，可得直线
斜率，和直线方程；根据直线n与C只有一个公共点，设出直线
方程，联立抛物线方程，
，可求得方程；据此利用点到直线距离公式求得距离之比.
（1）由对称性以及
可知
是等边三角形.
又F点到MN的距离为，故
，
由抛物线定义知：点A到准线l的距离
又
.
故抛物线方程为：.
（2）由对称性设
，则
点A，M关于点F对称，得
，
得：
，直线m斜率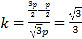
，
所以直线m方程为
.
∵
，设直线n方程为：
，
又因为直线n与抛物线只有一个公共点，
所以
，消去
得
，
由
，得
直线
，
坐标原点到n，m距离的比值为
.
练习册系列答案
相关题目
【题目】足球是世界普及率最高的运动，我国大力发展校园足球.为了解本地区足球特色学校的发展状况，社会调查小组得到如下统计数据：
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色学校y（百个） | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
（1）根据上表数据，计算y与x的相关系数r，并说明y与x的线性相关性强弱.
（已知：
，则认为y与x线性相关性很强；
，则认为y与x线性相关性一般；
，则认为y与x线性相关性较）：
（2）求y关于x的线性回归方程，并预测A地区2020年足球特色学校的个数（精确到个）.
参考公式和数据：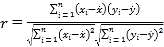
，
，
.
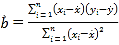
