题目内容
（2012•汕头一模）在△ABC中，∠BAC=120°，AB=AC=2，D为BC边上的点，且
•
=0，若
=3
，则(
+
)•
| AD |
| BC |
| CE |
| EB |
| AB |
| AC |
| AE |
2
2
．分析：由
•
=0，可得D是底边BC的中点，由
=3
可得E是BC的一个四等分点，再根据等腰三角形的性质易知∠BAD=60°，根据含30度角的直角三角形的性质结合向量数量积的运算可得答案．
| AD |
| BC |
| CE |
| EB |
解答：
解：∵△ABC中，AB=AC，∠BAC=120°，
由
•
=0，知AD⊥BC于D，且D是BC的中点，
∴
+
=2
∴∠BAD=60°，又AB=AC=2，
∴CD=BD=
，AD=1
∵
=3
，
∴E是BC的一个四等分点，且CE=3EB，
∴DE=
，
∴(
+
)•
=2
•
=2|
| |
| cos∠DAE
∵在直角三角形ADE中，|
| =|
| cos∠DAE，
∴上式=2|
| ×|
|=2×1×1=2．
故答案为：2．
解：∵△ABC中，AB=AC，∠BAC=120°，由
| AD |
| BC |
∴
| AB |
| AC |
| AD |
∴∠BAD=60°，又AB=AC=2，
∴CD=BD=
| 3 |
∵
| CE |
| EB |
∴E是BC的一个四等分点，且CE=3EB，
∴DE=
| ||
| 2 |
∴(
| AB |
| AC |
| AE |
| AD |
| AE |
| AD |
| AE |
∵在直角三角形ADE中，|
| AD |
| AE |
∴上式=2|
| AD |
| AD |
故答案为：2．
点评：本题考查了向量在几何中的应用、平面向量数量积的运算、等腰三角形的性质和含30度角的直角三角形的性质，要熟练掌握好边角之间的关系．
练习册系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
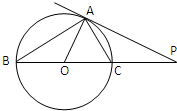（2012•汕头一模）（几何证明选讲选做题）已知PA是⊙O的切线，切点为A，直线PO交⊙O于B、C两点，AC=2，∠PAB=120°，则⊙O的面积为
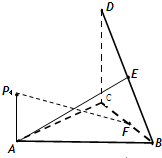（2012•汕头一模）如图，直角△BCD所在的平面垂直于正△ABC所在的平面，PA⊥平面ABC，DC=BC=2PA，E为DB的中点．
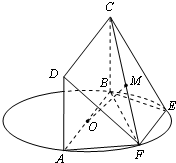（2012•汕头一模）如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD所在的平面和圆O所在的平面互相垂直，且AB=2，AD=EF=1．