Question

【题目】已知数列中各项都大于1，前项和为，且满足.

（1）求数列的通项公式；

（2）令，求数列的前项和；

（3）求使得对所有都成立的最小正整数.

Answer 1

【答案】（1）；（2）；（3）.

【解析】

试题分析：（1）首先令，利用,求解数列的首项，再令，得到，然后两式相减，得到数列的递推公式，可知数列是等差数列，写出通项公式；（2）根据上一问的结果，代入可得数列的通项公式，采用裂项相消法求和；（3）对恒成立的问题，可转化为，从而求得最小正整数.

试题解析：（1）当 时，，

解之得，（舍去）

由 ①

得 ②

②-①得

即

由于，故

可见数列为等差数列，公差是3，首项是2，

所以.

（2），

所以

即数列的前项和.

（3） 使得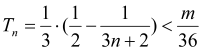对所有都成立的必须满足，即，故满足要求的最小正整数为6.