题目内容
(本小题满分12分)设函数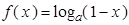 ,
,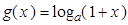 (
(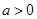 且
且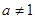 )。
)。
(1)设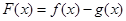 ,判断
,判断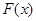 的奇偶性并证明;
的奇偶性并证明;
(2)若关于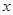 的方程
的方程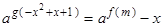 有两个不等实根,求实数
有两个不等实根,求实数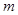 的范围;
的范围;
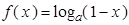 ,
,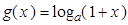 (
(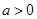 且
且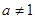 )。
)。(1)设
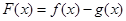 ,判断
,判断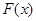 的奇偶性并证明;
的奇偶性并证明;(2)若关于
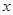 的方程
的方程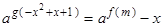 有两个不等实根,求实数
有两个不等实根,求实数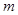 的范围;
的范围;(3)若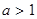 且在
且在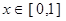 时,
时,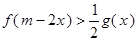 恒成立,求实数
恒成立,求实数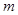 的范围。(1)
的范围。(1)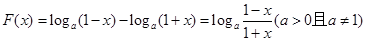
其中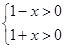 ∴
∴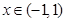
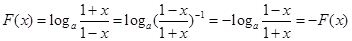
∴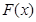 为奇函数。
为奇函数。
(2)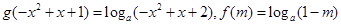
原方程有两个不等实根即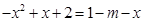 有两个不等实根。
有两个不等实根。
其中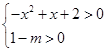 ∴
∴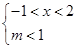 即
即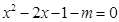 在
在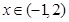 上有两个不等实根。 记
上有两个不等实根。 记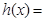
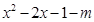 ,对
,对 称轴x=1,由
称轴x=1,由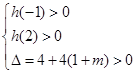 解得
解得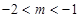 .
.
(3)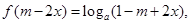
即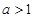 且
且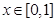 时
时 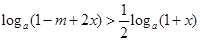 恒成立
恒成立
∴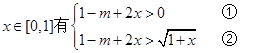 恒成立,
恒成立,
由①得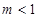
令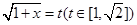 ∴由②得
∴由②得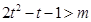 在
在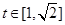 时恒成立
时恒成立
记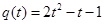 即
即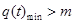 ,
,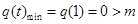
综上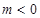
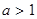 且在
且在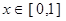 时,
时,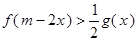 恒成立,求实数
恒成立,求实数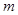 的范围。(1)
的范围。(1)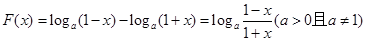
其中
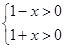 ∴
∴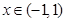
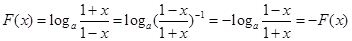
∴
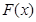 为奇函数。
为奇函数。 (2)
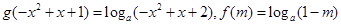
原方程有两个不等实根即
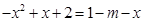 有两个不等实根。
有两个不等实根。其中
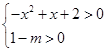 ∴
∴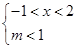 即
即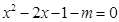 在
在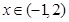 上有两个不等实根。 记
上有两个不等实根。 记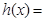
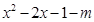 ,对
,对 称轴x=1,由
称轴x=1,由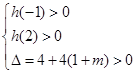 解得
解得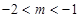 .
. (3)
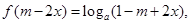
即
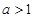 且
且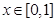 时
时 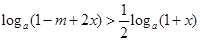 恒成立
恒成立∴
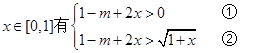 恒成立,
恒成立, 由①得
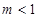
令
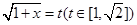 ∴由②得
∴由②得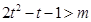 在
在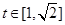 时恒成立
时恒成立记
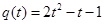 即
即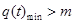 ,
,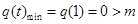
综上
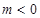
略

练习册系列答案
相关题目
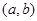
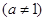 在函数
在函数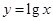 的图像上,,则下列点也在此图像上的是( )
的图像上,,则下列点也在此图像上的是( )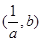
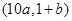

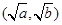
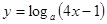 ,(a>0且a≠1) 图象必过的定点是
,(a>0且a≠1) 图象必过的定点是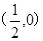
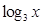 ,求函数y=
,求函数y=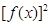 +
+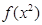 ,x∈
,x∈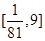 的最大值与最小值.
的最大值与最小值.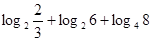 = .
= .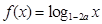 在
在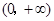 上单调递减,则实数
上单调递减,则实数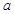 的取值范围是 .
的取值范围是 .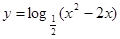 的单调递减区间是 .
的单调递减区间是 .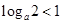 ,则
,则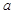 的取值范围是
的取值范围是  ,若
,若 ,则
,则
 的值等于 .
的值等于 .