Question

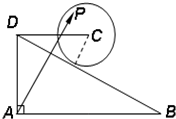如图，在直角梯形ABCD中，AD⊥AB，AB∥DC，AD=DC=1，AB=2，动点P在以点C为圆心，且与直线BD相切的圆上或圆内移动，设

AP

=λ

AD

+μ

AB

（λ，μ∈R），则λ+μ取值范围是

 

．

Answer 1

分析：以A为坐标原点建立如图所示直角坐标系，可得直线BD的方程x+2y-2=0．算出点C到BD的距离d=

5

5

，得到以点C为圆心且与直线BD相切的圆方程为（x-1）²+（y-1）²=

1

5

．设P（x，y），根据题中的向量等式算出P的坐标为（2μ，λ），由P在圆内或圆上得到（2μ-1）²+（λ-1）²≤

1

5

．将此不等式化成关于λ的一元二次不等式，利用根的判别式加以计算，可得λ+μ取值范围．

解答：解：以A为坐标原点，AB、AD所在直线为x轴、y轴，建立平面直角坐标系如图所示．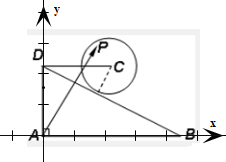
则A（0，0），D（0，1），C（1，1），B（2，0）
直线BD的方程为

x

2

+

y

1

=1，化简得x+2y-2=0，
∴点C到BD的距离d=

|1+2-2|

5

=

5

5

，
可得以点C为圆心，且与直线BD相切的圆方程为
（x-1）²+（y-1）²=

1

5

．
设P（x，y），则

AP

=（x，y），

AD

=（0，1），

AB

=（2，0），
∵

AP

=λ

AD

+μ

AB

（λ，μ∈R），
∴（x，y）=λ（0，1）+μ（2，0）=（2μ，λ），
可得x=2μ且y=λ，P的坐标为（2μ，λ）．
∵P在圆内或圆上，
∴（2μ-1）²+（λ-1）²≤

1

5

，
设λ+μ=t，得μ=t-λ，
代入上式化简整理得5λ²-（8t-2）λ+4t²-4t+

9

5

≤0，
若要上述不等式有实数解，
则△=（8t-2）²-4×5×（4t²-4t+

9

5

）≥0，
化简得t²-3t+2≤0，
解得1≤t≤2，
即1≤λ+μ≤2，
∴λ+μ取值范围是[1，2]．
故答案为：[1，2]

点评：本题在直角梯形中给出满足条件的向量式，求参数的取值范围．着重考查了直线的方程、点到直线的距离公式、圆的标准方程、直线与圆的位置关系与向量的坐标运算等知识，属于中档题．同时考查了逻辑推理能力与计算能力，考查了数形结合、转化化归的数学思想，是一道不错的综合题．