Question

若集合M={x|x²+x-6=0}，N={x|ax-1=0，a≠0}，且N⊆M，则实数a的值为________．

Answer 1

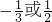
分析：本题考查的知识点是集合的包含关系判断及应用，由a≠0，则N为非空集合，N⊆M则说明N的元素是M的元素，由M={x|x²+x-6=0}解出集合M后，易得到满足条件的实数a的值．
解答：∵M={x|x²+x-6=0}，
∴M={-3，2}
又∵N={x|ax-1=0，a≠0}≠∅
又∵N⊆M，
∴a=
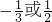
故答案为：
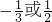
点评：集合N⊆M，说明N为空集或N的元素都为M的元素，本题中由a≠0，N≠∅，不需要分类讨论，但如果没有此限制，则要分N=∅和N≠∅两种情况讨论．