题目内容
设集合A={x|2lgx=lg(8x-15),x∈R},B={x|cos| x | 2 |
分析:根据对数的运算法则化简集合A得到集合A的元素,由余弦函数的图象和周期性得到满足集合B的元素,求出两集合的交集即可知道交集中元素的个数.
解答:解:根据集合A得到:2lgx=lg(8x-15)即x2-8x+15=0,
(x-3)(x-5)=0,
所以x=3,x=5,
则集合A={3,5};
根据集合B得到:cos
>0得到
∈(2kπ-
,2kπ+
),
所以x∈(4kπ-π,4kπ+π)
则A∩B={5},所以∩B的元素个数为1个.
故答案为1.
(x-3)(x-5)=0,
所以x=3,x=5,
则集合A={3,5};
根据集合B得到:cos
| x |
| 2 |
| x |
| 2 |
| π |
| 2 |
| π |
| 2 |
所以x∈(4kπ-π,4kπ+π)
则A∩B={5},所以∩B的元素个数为1个.
故答案为1.
点评:本题属于以对数函数与三角函数为平台,求集合的交集的基础题,是高考中常考的内容.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 >0,x∈R},则A∩B的元素个数为 个.
>0,x∈R},则A∩B的元素个数为 个.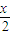 >0,x∈R},则A∩B的元素个数为 个.
>0,x∈R},则A∩B的元素个数为 个.