题目内容
在约束条件 下,目标函数z=2x+3y的最小值为 ,最大值为 .
下,目标函数z=2x+3y的最小值为 ,最大值为 .
【答案】分析:可分成三个步骤:①作出可行域,②z为目标函数纵截距的三分之一,③画直线2x+3y=0,平移直线观察最值.
解答: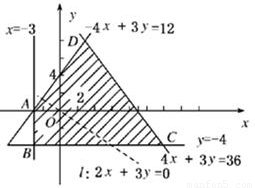 解:作出可行域(如图阴影部分).
解:作出可行域(如图阴影部分).
令z=0,作直线l:2x+3y=0.
当把直线l向下平移时,所对应的z=2x+3y的值随之减小,所以,直线经过可行域的顶点B时,z=2x+3y取得最小值.
从图中可以看出,顶点B是直线x=-3与直线y=-4的交点,其坐标为(-3,-4);
当把l向上平移时,所对应的z=2x+3y的值随之增大,所以直线经过可行域的顶点D时,z=2x+3y取得最大值.
顶点 D是直线-4x+3y=12与直线4x+3y=36的交点,
解方程组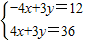 ,可以求得顶点D的坐标为(3,8).
,可以求得顶点D的坐标为(3,8).
所以zmin=2×(-3)+3×(-4)=-18,zmax=2×3+4×8=30.
故答案为:-18,30.
点评:本题考查不等式中的线性规划知识,画出平面区域与正确理解目标函数的几何意义是解答好本题的关键.
解答:
 解:作出可行域(如图阴影部分).
解:作出可行域(如图阴影部分).令z=0,作直线l:2x+3y=0.
当把直线l向下平移时,所对应的z=2x+3y的值随之减小,所以,直线经过可行域的顶点B时,z=2x+3y取得最小值.
从图中可以看出,顶点B是直线x=-3与直线y=-4的交点,其坐标为(-3,-4);
当把l向上平移时,所对应的z=2x+3y的值随之增大,所以直线经过可行域的顶点D时,z=2x+3y取得最大值.
顶点 D是直线-4x+3y=12与直线4x+3y=36的交点,
解方程组
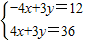 ,可以求得顶点D的坐标为(3,8).
,可以求得顶点D的坐标为(3,8).所以zmin=2×(-3)+3×(-4)=-18,zmax=2×3+4×8=30.
故答案为:-18,30.
点评:本题考查不等式中的线性规划知识,画出平面区域与正确理解目标函数的几何意义是解答好本题的关键.

练习册系列答案
相关题目
 下,目标函数z=x+5y的最大值为 .
下,目标函数z=x+5y的最大值为 .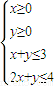 下,目标函数z=3x+2y的最大值是 .
下,目标函数z=3x+2y的最大值是 .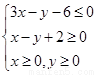 下
,目标函数
下
,目标函数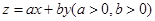 的最大值为12.给出下列四个判断:
的最大值为12.给出下列四个判断: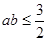 ; ②
; ②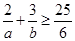 ; ③
; ③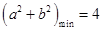 ; ④
; ④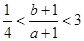 .
.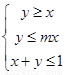 下,目标函数z=x+my的最大值小于2,则m的取值
下,目标函数z=x+my的最大值小于2,则m的取值 ,在约束条件
,在约束条件 下,目标函数
下,目标函数 的最大值小于2,则
的最大值小于2,则 的取值范围为( )
的取值范围为( ) B.
B. C.
C. D.
D.