Question

已知函数f（x）=ax²+bx-1（a，b∈R且a＞0）有两个零点，其中一个零点在区间（1，2）内，则a-b的取值范围为

（-2，1）

．

Answer 1

分析：由零点的判定定理得到关于a、b的不等式组，把问题转化为线性规划问题，从而可以求最值

解答：解：由题意知，∵a＞0
∴f（x）的图象为开口向上的抛物线
又∵f（x）的截距为-1，且有一个零点在（1，2）
∴由勘根定理得：

f(1)＜0 f(2)＞0

，即

a+b-1＜0 4a+2b-1＞0

又a＞0
画出不等式组

a＞0 a+b-1＜0 4a+2b-1＞0

表示的区域如图：

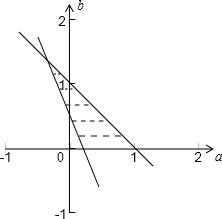
设z=a-b
∴b=a-z，得到一簇斜率为1，截距为-z的平行线
∴当直线b=a-z过a+b-1=0与4a+2b-1=0的交点时截距最大，z最小
过a+b-1=0与x轴的交点时截距最小，z最大
又

a+b-1=0 4a+2b-1=0

∴a=-

1

2

，b=-

3

2

a+b-1=0 b=0

∴a=1，b=0
∴a-b的最大值为：1-0=1
最小值为：-

1

2

-

3

2

=-2
∴a-b的取值范围为：（-2，1）
故答案为：（-2，1）

点评：本题考查零点的性质和线性规划问题，须根据条件得到约束条件，准确画出可行域．属简单题