题目内容
如图12，BC切△AEF的外接圆O于D，且EF∥BC.求证：AD平分∠BAC.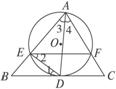
图12
思路分析:根据BC是切线，有∠1=∠3，∠2与∠4是同弧上的圆周角，所以相等，EF∥BC可以得到∠1=∠2，于是可得结论.
证明:∵BC是⊙O的切线，∴∠1=∠3.
∵∠2与∠4是同弧上的圆周角，∴∠2=∠4.
∵EF∥BC，∴∠1=∠2.
∴∠3=∠4，即AD平分∠BAC.
练习册系列答案
阅读快车系列答案
相关题目
如图，在棱长为2的正方体ABCD-A1B1C1D1内有一个内切球O，则过棱AA1和BC的中点P、Q的直线被球面截在球内的线段MN的长为（ ）A、2(
| ||||
B、
| ||||
C、
| ||||
D、
|
