题目内容
过点（0，1）与双曲线x2-y2=1有且只有一个公共点的直线有（ ）A．2条
B．3条
C．4条
D．6条
【答案】分析：用代数法，先联立方程，消元后得到一个方程，先研究相切的情况，即判别式等于零，再研究与渐近线平行的情况．
解答：解：设过点（0，1）与双曲线x2-y2=1有且只有一个公共点的直线为y=kx+1．
根据题意：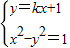
，
消去y整理得（1-k2）x2-2kx-5=0，
∵△=0，
∴k=±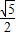
；
又注意直线恒过点（0，-1）且渐近线的斜率为±1，
与渐近线平行时也成立．
故过点（0，1）与双曲线x2-y2=1有且只有一个公共点的直线有4条．
故选C．
点评：本题主要考查直线与双曲线的位置关系，在只有一个公共点时，不要忽视了与渐近线平行的情况．
解答：解：设过点（0，1）与双曲线x2-y2=1有且只有一个公共点的直线为y=kx+1．
根据题意：
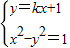，消去y整理得（1-k2）x2-2kx-5=0，
∵△=0，
∴k=±
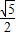；又注意直线恒过点（0，-1）且渐近线的斜率为±1，
与渐近线平行时也成立．
故过点（0，1）与双曲线x2-y2=1有且只有一个公共点的直线有4条．
故选C．
点评：本题主要考查直线与双曲线的位置关系，在只有一个公共点时，不要忽视了与渐近线平行的情况．
练习册系列答案
相关题目
+
=1，（a＞b＞0）与双曲4x2-
y2=1有相同的焦点，且椭C的离心e=
，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．
+
=1，（a＞b＞0）与双曲4x2-
y2=1有相同的焦点，且椭C的离心e=
，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．
+
=1，（a＞b＞0）与双曲4x2-
y2=1有相同的焦点，且椭C的离心e=
，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．
+
=1，（a＞b＞0）与双曲4x2-
y2=1有相同的焦点，且椭C的离心e=
，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．