题目内容
A、B是双曲线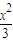 -y2=1上两点,M为该双曲线右准线上一点,且
-y2=1上两点,M为该双曲线右准线上一点,且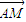 =
= .
.(Ⅰ)求|
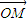 |的取值范围(O为坐标原点);
|的取值范围(O为坐标原点);(Ⅱ)求|
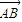 |的最小值.
|的最小值.
【答案】分析:(Ⅰ)由于M为该双曲线右准线上一点,故可得M( ,m),由
,m),由 =
= ,知M为AB的中点,进而假设直线方程与双曲线方程联立,利用直线与双曲线有两个不同的交点,可求的参数的范围,进而可确定|
,知M为AB的中点,进而假设直线方程与双曲线方程联立,利用直线与双曲线有两个不同的交点,可求的参数的范围,进而可确定| |的取值范围;
|的取值范围;
(Ⅱ)利用弦长公式可得| |2=(1+k2)(x1-x2)2=(1+k2)=
|2=(1+k2)(x1-x2)2=(1+k2)= ,根据基本不等式有4k2(1-3k2)≤(
,根据基本不等式有4k2(1-3k2)≤( )2=
)2= ,从而可求|
,从而可求| |取得最小值.
|取得最小值.
解答:解:(Ⅰ)双曲线的右准线方程为x= ,记M(
,记M( ,m),并设A(x1,y1),B(x2,y2).
,m),并设A(x1,y1),B(x2,y2).
由 =
= ,知M为AB的中点,则直线AB的斜率k存在,且k≠0,于是直线AB的方程为y=k(x-
,知M为AB的中点,则直线AB的斜率k存在,且k≠0,于是直线AB的方程为y=k(x- )+m,
)+m,
代入双曲线方程,并整理得(1-3k2)x2+3k(3k-2m)x- (3k-2m)2-3=0
(3k-2m)2-3=0
因为 1-3k2≠0,x1+x2=3,
所以 ,∴
,∴ ,
,
△=9 k2(3k-2m)2+3(1-3k2)[(3k-2m)2-3]=
由△>0,得 0<k2< ,所以m2>
,所以m2> .
.
因为| |=
|= ,
,
故| |的取值范围为(
|的取值范围为( ,+∞).
,+∞).
(Ⅱ)| |2=(1+k2)(x1-x2)2=(1+k2)=
|2=(1+k2)(x1-x2)2=(1+k2)=
因为4k2(1-3k2)≤( )2=
)2=
所以| |2≥
|2≥ =48,当且仅当k2=
=48,当且仅当k2= 时取“=”号.
时取“=”号.
故当k=± 时,|
时,| |取得最小值4
|取得最小值4 .
.
点评:本题以双曲线为载体,考查直线与双曲线的位置关系,考查基本不等式的运用,解题的关键是将直线与双曲线方程联立,利用韦达定理求解.
 ,m),由
,m),由 =
= ,知M为AB的中点,进而假设直线方程与双曲线方程联立,利用直线与双曲线有两个不同的交点,可求的参数的范围,进而可确定|
,知M为AB的中点,进而假设直线方程与双曲线方程联立,利用直线与双曲线有两个不同的交点,可求的参数的范围,进而可确定| |的取值范围;
|的取值范围;(Ⅱ)利用弦长公式可得|
 |2=(1+k2)(x1-x2)2=(1+k2)=
|2=(1+k2)(x1-x2)2=(1+k2)= ,根据基本不等式有4k2(1-3k2)≤(
,根据基本不等式有4k2(1-3k2)≤( )2=
)2= ,从而可求|
,从而可求| |取得最小值.
|取得最小值.解答:解:(Ⅰ)双曲线的右准线方程为x=
 ,记M(
,记M( ,m),并设A(x1,y1),B(x2,y2).
,m),并设A(x1,y1),B(x2,y2).由
 =
= ,知M为AB的中点,则直线AB的斜率k存在,且k≠0,于是直线AB的方程为y=k(x-
,知M为AB的中点,则直线AB的斜率k存在,且k≠0,于是直线AB的方程为y=k(x- )+m,
)+m,代入双曲线方程,并整理得(1-3k2)x2+3k(3k-2m)x-
 (3k-2m)2-3=0
(3k-2m)2-3=0因为 1-3k2≠0,x1+x2=3,
所以
 ,∴
,∴ ,
,△=9 k2(3k-2m)2+3(1-3k2)[(3k-2m)2-3]=

由△>0,得 0<k2<
 ,所以m2>
,所以m2> .
.因为|
 |=
|= ,
,故|
 |的取值范围为(
|的取值范围为( ,+∞).
,+∞).(Ⅱ)|
 |2=(1+k2)(x1-x2)2=(1+k2)=
|2=(1+k2)(x1-x2)2=(1+k2)=
因为4k2(1-3k2)≤(
 )2=
)2=
所以|
 |2≥
|2≥ =48,当且仅当k2=
=48,当且仅当k2= 时取“=”号.
时取“=”号.故当k=±
 时,|
时,| |取得最小值4
|取得最小值4 .
.点评:本题以双曲线为载体,考查直线与双曲线的位置关系,考查基本不等式的运用,解题的关键是将直线与双曲线方程联立,利用韦达定理求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 -y2=1上两点,M为该双曲线右准线上一点,且
-y2=1上两点,M为该双曲线右准线上一点,且 =
= .
. |的取值范围(O为坐标原点);
|的取值范围(O为坐标原点); |的最小值.
|的最小值.