题目内容
已知向量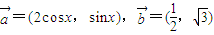 ,
,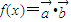 ,下面关于的说法中正确的是( )
,下面关于的说法中正确的是( )A.函数f(x)最小正周期是π
B.函数f(x)在区间
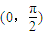 为增函数
为增函数C.函数f(x)的图象关于直线
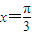 对称
对称D.函数f(x)图象可由函数y=2sinx向右平移
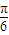 个单位长度得到
个单位长度得到
【答案】分析:先利用向量的数量积公式化简f(x);利用三角函数的周期公式判断出A错;通过整体角处理的方法求出f(x)的递增区间判断出B错;通过整体角处理的方法求出函数的对称轴判断出C对;通过图象平移的规律判断出D错.
解答:解:因为向量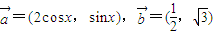 ,
,
所以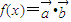 =cosx+
=cosx+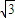 sinx=2sin(x+
sinx=2sin(x+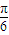 ),
),
对于A,函数的最小正周期为π;故A错;
对于B,单调增区间为2k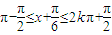 即
即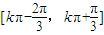 故B错;
故B错;
对于C,对称轴为x+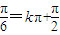 即x=
即x=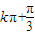 ,当k=0时,对称轴为x=
,当k=0时,对称轴为x=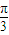 ;
;
对于D,函数y=2sinx向右平移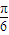 个单位长度得到y=2sin(x-
个单位长度得到y=2sin(x-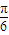 ),故D错,
),故D错,
故选C.
点评:本题考查向量的数量积公式,三角函数的周期公式,整体角处理的方法来研究三角函数的性质问题,属于中档题.
解答:解:因为向量
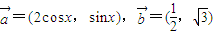 ,
,所以
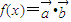 =cosx+
=cosx+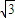 sinx=2sin(x+
sinx=2sin(x+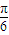 ),
),对于A,函数的最小正周期为π;故A错;
对于B,单调增区间为2k
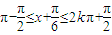 即
即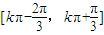 故B错;
故B错;对于C,对称轴为x+
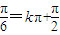 即x=
即x=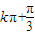 ,当k=0时,对称轴为x=
,当k=0时,对称轴为x=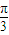 ;
;对于D,函数y=2sinx向右平移
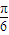 个单位长度得到y=2sin(x-
个单位长度得到y=2sin(x-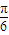 ),故D错,
),故D错,故选C.
点评:本题考查向量的数量积公式,三角函数的周期公式,整体角处理的方法来研究三角函数的性质问题,属于中档题.

练习册系列答案
相关题目
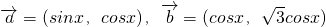 ,
,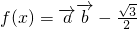 ,下面关于函数f(x)的导函数f'(x)说法中错误的是
,下面关于函数f(x)的导函数f'(x)说法中错误的是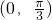 为减函数
为减函数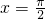 对称
对称 个单位长度得到
个单位长度得到 ,
, ,下面关于函数f(x)的导函数f'(x)说法中错误的是( )
,下面关于函数f(x)的导函数f'(x)说法中错误的是( ) 为减函数
为减函数 对称
对称 个单位长度得到
个单位长度得到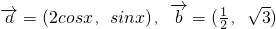 ,
, ,下面关于的说法中正确的是
,下面关于的说法中正确的是 为增函数
为增函数 对称
对称 个单位长度得到
个单位长度得到