题目内容
已知函数f(x)=
是偶函数,直线y=t与函数f(x)的图象自左至右依次交于四个不同点A、B、C、D,若|AB|=|BC|,则实数t的值为 .
|
分析:根据函数f(x)是偶函数,得到a,b,c的值,然后根据二次函数的图象的对称性,解出A,B,C,D的坐标,利用|AB|=|BC|,即可求出实数t的值.
解答:解:∵函数f(x)是偶函数,
∴f(-x)=f(x),
当x<0时,-x>0,
即f(-x)=ax2-2x+1=-x2+bx+c,
∴a=-1,b=-2,c=1,
即f(x)=
,
作出函数f(x)的图象如图: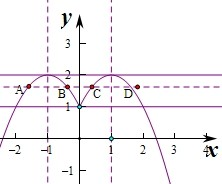
直线y=t与函数f(x)的图象自左至右依次交于四个不同点A、B、C、D,
不妨是对应的横坐标分别为a,b,c,d,
则A,B关于x=-1对称,即
=-1,①
∵函数是偶函数,∴c=-b,d=-a,
若|AB|=|BC|,
则B是A,B的中点,
∴
=
=b,②,
解得a=3b,代入①
解得b=-
,a=-
,
当b=-
,时f(b)=f(-
)=-(-
)2-2(-
)+1=2-
=
,
即t=
,
故答案为:
.
∴f(-x)=f(x),
当x<0时,-x>0,
即f(-x)=ax2-2x+1=-x2+bx+c,
∴a=-1,b=-2,c=1,
即f(x)=
|
作出函数f(x)的图象如图:

直线y=t与函数f(x)的图象自左至右依次交于四个不同点A、B、C、D,
不妨是对应的横坐标分别为a,b,c,d,
则A,B关于x=-1对称,即
| a+b |
| 2 |
∵函数是偶函数,∴c=-b,d=-a,
若|AB|=|BC|,
则B是A,B的中点,
∴
| a+c |
| 2 |
| a-b |
| 2 |
解得a=3b,代入①
解得b=-
| 1 |
| 2 |
| 3 |
| 2 |
当b=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 7 |
| 4 |
即t=
| 7 |
| 4 |
故答案为:
| 7 |
| 4 |
点评:本题主要考查函数奇偶性的应用,以及二次函数的图象和性质,利用数形结合是解决本题的关键,考查中点坐标公式,综合性较强.

练习册系列答案
相关题目
已知函数f(x)=a-
,若f(x)为奇函数,则a=( )
| 1 |
| 2x+1 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |