题目内容
求函数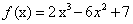 的单调区间和极值.
的单调区间和极值.
解:f′(x)=6x2-12x,令f′(x)>0,即6x2-12x>0,解得x<0或x>2.
同理,由f′(x)<0,解得0<x<2.
∴函数的单调增区间为(-∞,0)和(2,+∞),单调减区间为(0,2).列表
| x | (-∞,0) | 0 | (0,2) | 2 | (2,+∞) |
| f’(x) | + | 0 | - | 0 | + |
| f(x) | 增 | 7 | 减 | -1 | 增 |
∴当x=0时,f(x)取极大值f(0)=7,
当x=2时,f(x)取极小值f(2)=-1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

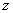 的模等于2,则
的模等于2,则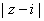 的最大值等于( )
的最大值等于( ) 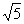 D.3
D.3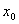 附近的左侧
附近的左侧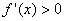 右侧
右侧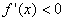 那么
那么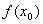 是极大值
是极大值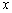 的函数
的函数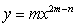 的导数为
的导数为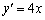 ,则
,则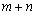 的值为__________
的值为__________ 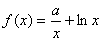 ,
, 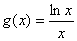 ,
,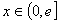 ,其中e是无理数且e=2.71828…,
,其中e是无理数且e=2.71828…,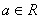 .
.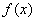 的单调区间与极值;
的单调区间与极值;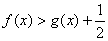 ;
; -1 B. 2
-1 B. 2 在区间上的零点的个数为 ( )
在区间上的零点的个数为 ( )