题目内容
【题目】设等差数列![]() 的公差为
的公差为![]() 前
前![]() 项和为
项和为![]() 且
且![]() 则
则![]() 的取值范围是_________.
的取值范围是_________.
【答案】![]()
【解析】
利用等差数列通项公式和求和公式可得到不等式组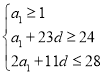 ,将
,将![]() 看成关于
看成关于![]() 的函数,从而所求范围变为求解
的函数,从而所求范围变为求解![]() 的范围.由不等式组可得可行域,由二次函数性质可确定
的范围.由不等式组可得可行域,由二次函数性质可确定![]() 中
中![]() 的最大值和最小值分别在动点
的最大值和最小值分别在动点![]() 落在直线
落在直线![]() 和
和![]() 上时取得;利用直线方程可将所求式子化为二次函数形式,利用二次函数值域的求解方法可求得
上时取得;利用直线方程可将所求式子化为二次函数形式,利用二次函数值域的求解方法可求得![]() 的范围,即为
的范围,即为![]() 的范围.
的范围.
由题意得: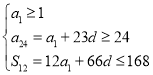 ,即
,即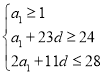
![]()
将![]() 看成关于
看成关于![]() 的函数,即
的函数,即![]() ,
,![]()
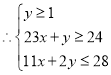
求![]() 得范围即求
得范围即求![]() 的范围
的范围
由不等式组可得动点![]() 构成的可行域如下图阴影部分(含边界)所示:
构成的可行域如下图阴影部分(含边界)所示:
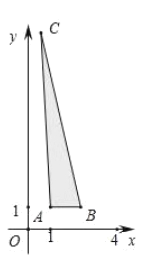
则![]() ,
,![]() ,
,![]()
设![]() ,则
,则![]()
由二次函数性质可知,对于每一个固定的![]() ,当
,当![]() 越接近
越接近![]() 时
时![]() 越大;当
越大;当![]() 越远离
越远离![]() 时,
时,![]() 越小
越小
![]() 要使
要使![]() 取最小值,则
取最小值,则![]() 必在直线
必在直线![]() 上
上
当![]() 时,
时,![]() ,
,![]()
![]()
要使![]() 取最大值,则
取最大值,则![]() 必在直线
必在直线![]() 上
上
当![]() 时,
时,![]() ,
,![]()
![]()
综上所述:![]() 的取值范围为
的取值范围为![]()
故答案为:![]()

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目