题目内容
若
，
，且
与
垂直，则向量
与
的夹角大小为 ．
【答案】分析：利用两个向量垂直的性质可得（ 
）•
=0，求得cosθ 的值，进而求得θ的值．
解答：解：设向量
与
的夹角大小为θ，则由题意可得（ 
）•
=
+
+=1+1×2×cosθ=0，
∴cosθ=-
．
再由 0≤θ＜π可得 θ=
，
故答案为
．
点评：本题主要考查两个向量的数量积的定义，两个向量垂直的性质，根据三角函数的值求角，属于中档题．
）•=0，求得cosθ 的值，进而求得θ的值．解答：解：设向量
与的夹角大小为θ，则由题意可得（ ）•=++=1+1×2×cosθ=0，∴cosθ=-
．再由 0≤θ＜π可得 θ=
，故答案为
．点评：本题主要考查两个向量的数量积的定义，两个向量垂直的性质，根据三角函数的值求角，属于中档题．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
若平面向量
=(-5，4)，
=(-4，-5)，则
与
（ ）
| a |
| b |
| a |
| b |
| A、平行且同向 | B、平行且反向 |
| C、垂直 | D、不垂直也不平行 |
；
，则直线
与直线
相互垂直；
，使得
”的否定是“
，都有
”；
的图象向右平移
个单位，得到函数
的图象。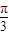
个单位，得到函数y=sin（2x-
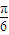）的图象．