题目内容
已知f（x）=ax+a-x（a＞0，a≠1），且f（1）=3．（1）求f（
）的值；（2）求f（0）+f（1）+f（2）的值．
【答案】分析：（1）f（x）=ax+a-x（a＞0，a≠1），且f（1）=3，然后利用整体代入法求解；
（2）根据（1）可以分别求出f（0）、f（1）和f（2）的值，再进行求解；
解答：解：（1）由f（1）=a1+a-1=3，
得[f（
）]2=a2+a-2=（a1+a-1） 2-2=5，…（3分）
又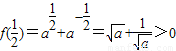
，
所以f（
）=
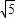…（6分）；
（2）f（0）=a+a=2…（8分）
f（1）=3
f（2）=a2+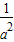
=（a+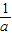
）2-2=9-2=7…（11分）
f（0）+f（1）+f（2）=2=2+3++7=12．…（12分）
点评：此题主要考查函数的值，解题的过程中用到了整体的思想，是一道基础题；
（2）根据（1）可以分别求出f（0）、f（1）和f（2）的值，再进行求解；
解答：解：（1）由f（1）=a1+a-1=3，
得[f（
）]2=a2+a-2=（a1+a-1） 2-2=5，…（3分）又
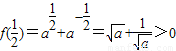，所以f（
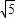）=…（6分）；（2）f（0）=a+a=2…（8分）
f（1）=3
f（2）=a2+
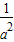=（a+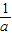）2-2=9-2=7…（11分）f（0）+f（1）+f（2）=2=2+3++7=12．…（12分）
点评：此题主要考查函数的值，解题的过程中用到了整体的思想，是一道基础题；
练习册系列答案
相关题目