题目内容
若函数 是定义在
是定义在 上的偶函数,在
上的偶函数,在 上是减函数,且
上是减函数,且 ,则使得
,则使得 的
的 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
A
解析试题分析:因为,函数 是定义在
是定义在 上的偶函数,在
上的偶函数,在 上是减函数,且
上是减函数,且 ,所以,函数在
,所以,函数在 是增函数,
是增函数, 。
。
X<-2或x>2时, ;
; 时,
时, 。故
。故 的
的 的取值范围是
的取值范围是 ,选A。
,选A。
考点:函数的奇偶性,函数的单调性,一元二次不等式的解法。
点评:小综合题,抽象不等式问题,往往要利用函数的单调性,结合函数的图象分析得解。本题较为典型。

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
设函数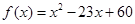 ,
, ,则
,则 ( )
( )
| A.0 | B.38 | C.56 | D.112 |
已知函数 ,则不等式
,则不等式 的解集为( )
的解集为( )
A. | B. | C. | D. |
已知函数 ,则函数
,则函数 的零点个数是( )
的零点个数是( )
| A.4 | B.3 | C.2 | D.1 |
已知函数 若
若 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
点A(a+b,ab)在第一象限内,则直线bx+ay-ab=0不经过的象限是( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
(5分)设函数 (a∈R,e为自然对数的底数),若曲线y=sinx上存在点(x0,y0)使得f(f(y0))=y0,则a的取值范围是( )
(a∈R,e为自然对数的底数),若曲线y=sinx上存在点(x0,y0)使得f(f(y0))=y0,则a的取值范围是( )
| A.[1,e] | B.[e﹣1﹣1,1] | C.[1,e+1] | D.[e﹣1﹣1,e+1] |
若存在正数x使2x(x-a)<1成立,则a 的取值范围是( )
| A.(-∞,+∞) | B.(-2, +∞) | C.(0, +∞) | D.(-1,+∞) |
 设
设 表示
表示 中的较大值,
中的较大值, 表示
表示 得最小值为
得最小值为
 得最小值为
得最小值为 ,则
,则



