题目内容
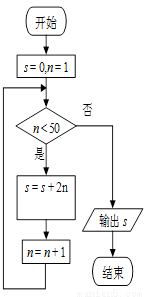
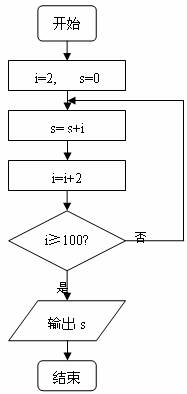
 下面的程序框图给出数列{an}(n∈N*),下同)的递推关系,计算并输出数列{an}和{
下面的程序框图给出数列{an}(n∈N*),下同)的递推关系,计算并输出数列{an}和{ }前若干项之和S、T.
}前若干项之和S、T.
(1)若输入p=1,S满足80<S<100,求输入的n的值;
(2)若输入p>1,n,求输出的T的值.
(用关于p、n的代数式表示)
(1)P=1时,an=an-1+1,
{an}(n∈N*)是首项为1,公差为1的等差数列…(1分),
所以an=n…(2分),
S=a1+a2+…+an= …(3分),
…(3分),
解得80<S<100,即160<n(n+1)<200,
∴ ,
,
∵n∈N*,
∴n=13.…(5分).
(2)P>1时,an+1=pan+1,
 …(7分),
…(7分),
∴ (n∈N*)是首项为1+
(n∈N*)是首项为1+ =
=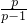 ,公比为p的等比数列…(8分),
,公比为p的等比数列…(8分),
所以 ,
,
 …(9分),
…(9分),
 ,…(11分),
,…(11分),
所以:
=
= .…(13分).
.…(13分).
分析:(1)P=1时,由an=an-1+1,知an=n,所以S=a1+a2+…+an= ,解得80<S<100,由此能求出n的值.
,解得80<S<100,由此能求出n的值.
(2)P>1时,an+1=pan+1, ,所以
,所以 ,
, ,
, ,由此能求出T的值.
,由此能求出T的值.
点评:本题以循环结构为载体,考查数列的应用,十分巧妙,体现了出题者的智慧,是一道好题.解题时要认真审题,注意递推公式的合理运用.
{an}(n∈N*)是首项为1,公差为1的等差数列…(1分),
所以an=n…(2分),
S=a1+a2+…+an=
 …(3分),
…(3分),解得80<S<100,即160<n(n+1)<200,
∴
 ,
,∵n∈N*,
∴n=13.…(5分).
(2)P>1时,an+1=pan+1,
 …(7分),
…(7分),∴
 (n∈N*)是首项为1+
(n∈N*)是首项为1+ =
=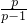 ,公比为p的等比数列…(8分),
,公比为p的等比数列…(8分),所以
 ,
, …(9分),
…(9分), ,…(11分),
,…(11分),所以:

=

=
 .…(13分).
.…(13分).分析:(1)P=1时,由an=an-1+1,知an=n,所以S=a1+a2+…+an=
 ,解得80<S<100,由此能求出n的值.
,解得80<S<100,由此能求出n的值.(2)P>1时,an+1=pan+1,
 ,所以
,所以 ,
, ,
, ,由此能求出T的值.
,由此能求出T的值.点评:本题以循环结构为载体,考查数列的应用,十分巧妙,体现了出题者的智慧,是一道好题.解题时要认真审题,注意递推公式的合理运用.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目